Electron--vibration coupling constants in positively charged fullerene.
home | group
Electron--vibration coupling constants in positively charged fullerene.home | group |

|
April 10, 2001
Recent breakthrough experiments (Schön et al. 2000) have shown that a monolayer of C60 can be positively field-doped, a goal hardly realized chemically so far (Datars and Ummat 1995). In that state, fullerene exhibits a higher resistivity than for negative doping, and becomes superconducting with critical temperatures that can exceed 50 K, about a factor 5 higher than the corresponding negative field-doped state. The general belief is that superconductivity in the fullerenes is related to a strong intra-molecular electron-phonon coupling, connected with the Jahn-Teller effect of the isolated ion (Antropov et al. 1993). Unlike the negative doping case, where both calculations (Antropov et al. 1993, Varma et al. 1991, Lannoo et al. 1991) and fits to data (Gunnarsson et al. 1995) exist, no quantitative evaluation of the actual Jahn-Teller coupling strengths is so far available for the positive fullerene ions.
In this work we undertake the task of determining the electron-vibration linear couplings for the Hu HOMO level of the C60 molecule, along with that of spelling out some of the consequences for resistivity and for superconductivity. For that purpose we use density functional electronic structure calculations, yielding accurate molecular vibration frequencies and eigenvectors for the two ag, six gg, and eight hg modes that couple linearly to the electronic Hu state. Knowing the form of the Jahn-Teller coupling matrices, we distort the molecule and extract the coupling constants from the calculated level shifts and splittings. As a parallel check, we repeat a similar calculation for the negative, electron doping case, where the ag and hg modes couple linearly to the T1u LUMO level of the C60 molecule. The couplings obtained for negatively doped C60 are rather similar to those that can be found in the literature, and just represent a fresher, state-of-the-art theoretical determination. The hole-vibration couplings of positively doped C60 are new, and can be put to use in a variety of manners, including predicting or explaining properties of molecular ions, such as photoemission (Brühwiler et al. 1997) and IR/Raman spectra. That is a task that we propose to consider in the near future.
The couplings obtained can also be used to determine the dimensionless electron-phonon coupling constant λ relevant for the superconductivity as well as for the vibron contribution to the high temperature T-linear resistivity in the crystalline phase. Comparing values for positive and negative doping we find that for positive doping λ is a factor 1.4 larger than for negative doping. These results provide a starting point for a discussion and comparison with the experimental findings.
This paper is organized as follows: the notation is set up in Sect. ham:sec; the ab-initio calculation and results for the molecular ion are described is Sect. dft:sec; in Sect. solid:sec we sketch the calculation of the resistivity in a band-degenerate case; Sect. superc:sec presents a formulation for superconductivity in that case; Sect. discussion:sec contains comparisons and discussion of experimental data.
Several theoretical papers (Ceulemans and Fowler 1990, De Los Rios et al. 1996, Moateet al. 1996, Moate et al. 1997, Manini and De Los Rios 2000) formulate the H × (a+g+h) Jahn-Teller (JT) and dynamical JT problem -- describing a hole in molecular C60 -- though with different notations and conventions. For ease of comparison, it is therefore useful to set up explicitly the conventions we use in the present calculation.
The analogies of the icosahedral
H × (a+g+h)
JT coupling to a spherical
D(2)× (D(0+) + D(2+) + D(4+))
model were exploited in earlier work, where among other things it was shown that surprisingly, and depending on numbers, this dynamical JT problem may or may not possess a Berry phase (De Los Rios et al. 1996, De Los Rios and Manini 1997, Manini and De Los Rios 1998). The representations
D(L±)
of
O(3)
map into representations of the icosahedral group
Ih
as follows (Altmann and Herzig 1994): D(0±) ---> ag/u, D(1±) ---> t1 g/u, D(2±) ---> hg/u, D(3±) ---> t2 g/u+ hg/u, D(4±) ---> gg/u+ hg/u, and so on. This means that the decomposition of the symmetric part of the tensor product
{ D(2-) × D(2-){}}s = D(0+) + D(2+) + D(4+)
becomes in icosahedral language
{ hu × hu {}}s = ag + hg + (gg + hg) .
ag
and
gg
appear only once, while the
hg
representation modes appears twice in this decomposition: one represents a genuine quadrupolar
D(2+)
state, while the other one derives from a
D(4+)
representation. Though this
O(3)
picture is suggestive (Ceulemans et al. 1994), clearly a quantitative description of C60n+ ions had better involve icosahedral symmetry from the beginning.
In the icosahedral group indeed in the hu × hu tensor product, the hg representation appears twice. This reflects the non-simple reducibility of the icosahedral symmetry group. Accordingly, Butler 1981 provides two independent sets of Clebsch-Gordan (CG) coefficients
hCµ,νm [r] = < H,µ;H,ν|h,m>[r]
which couple an
H
electronic state (quadratically) with an
h
vibrational mode (linearly) to give a scalar. Each set of coefficients is identified by a multiplicity index r=1,2. Since the two
h
states labeled
r=1,2
are symmetry-wise indistinguishable, the choice of these two sets of coefficients is perfectly arbitrary, as long as they are kept orthogonal to each other. This arbitrariness is the source of the different notations taken in the literature of this field. Here, we stick to Butler's choice (Butler 1981), which is basically equivalent to Ceulemans' convention (Fowler and Ceulemans 1985). Also, we label the states within a degenerate multiplet by the labels of the subgroup chain Ih \supset D5 \supset C5. For brevity, we indicate only the
C5
index
m
(m=0 for ag,
m=± 1,± 2
for
gg
and
m=-2,...,2
for
hg
states) in the labeling of states since, for the representations relevant to our problem, the
D5
label is just the absolute value of m.
Given the tabulated CG coefficients, it is necessary for generality to consider a linear combination
hCµ,νm(α)= cosα hCµ,νm [1] + sinα hCµ,νm [2]
of the two sets. The coefficient
hCµ,νm(α)
coincides with Butler's
r=1
and
r=2
values for
α=0
and
α=\/pi 2
respectively. Different values of
α
can be compared with the conventions of previous authors. For example,
α=-arctan( 3 / 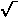 5 ) ~ -53.3°
is the case studied by De Los Rios et al. 1996 (where the
5 ) ~ -53.3°
is the case studied by De Los Rios et al. 1996 (where the
Ih
CG coefficient becomes equivalent to the spherical < 2,µ;2,ν|2,m>);
α=π/2
by Moate et al. 1996; and
α=0,π/2
by Ceulemans and Fowler 1990, where these cases are indicated as
hb
and
ha
respectively. The α-dependence of these CG coefficients indicates that -- unlike, for example, cubic symmetry -- belonging to the
hg
group representation in icosahedral symmetry does not determine completely the form of the JT coupling. The mixing angle
α
is also needed for that. In the present case of fullerene, each
hg
distortion mode is thus characterized not only by its frequency and scalar coupling, but also by its specific mixing angle -π/2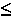 α
α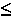 π/2.
π/2.
The basic linear Jahn-Teller Hamiltonian for the Hu× (ag+gg+hg) model is conveniently divided into:
H = Στ=ag,gg,hg Σinmodes(τ) [ Hharmτ(h ωτ i,\vec Pτ i,\vec Qτ i) + He-vτ (gτ i h ωτ i,ατ i,\vec Qτ i) ] .
The first term describes the linearly-coupled vibrations in the harmonic approximation,
Hharmτ(h ω,\vec P,\vec Q)= h ω /2 Σm (Pm2 +Qm2) ,
while the second term is the linear coupling to each mode:
He-vτ(g h ω ,α,\vec Q)= g h ω/2 Σm µ ν Qm c+µ c-ν τCµ,νm(α) .
Here, of course, the
α
dependence is relevant only for the
τ=hg
case. The distortion coordinates
Qτ i m
(with conjugate momentum Pτ i m) are dimensionless, being measured in units of x0(ωτ i) =(h / mC ωτ i)1/2. The operator
c+µ
creates an electron in orbital
µ(=-2,...,2)
of the HOMO
Hu
shell.
Naturally this form of the coupling Hamiltonian is such that each term represents pertinent irreducible representation combinations that are totally symmetrical, i.e., scalars, under the icosahedral group. For future applications, it will provide a convenient form both for perturbative calculations (small g values) and as a starting point for numerical diagonalization methods, such as the Lanczos technique. Here, however, we restrict ourselves to a study of the classical molecular distortions. For that, it is more convenient (Manini and De Los Rios 2000) to switch to a real representation of the vibrational degrees of freedom and orbitals.
To that end, we apply two standard unitary transformations (Manini and De Los Rios 2000), one to the electronic and the other to the vibrational degrees of freedom. We define a new set of electronic operators,
dm
(and consequently their Hermitian conjugates dm+), as
\begin{array} c0
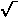 2 (
2 (
| 1 | i |
| 1 | -i |
He-vag(g h ω,q)= g h ω/2 q Σµ ν d+µ dν Vagµν ,
with Vagµν=δµν and q=Q0.
The second (similar) transformation is applied to the vibrational coordinates of the gg and hg modes:
\begin{array} Q0
modes only)
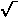 2 (
2 (
| 1 | i |
| 1 | -i |
He-vτ(g h ω ,α,\vec q )= g h ω/2 Σm qm Σµ ν d+µ dν Vτ (m)µ ν(α) \ \ (τ=gg,hg) .
The
5× 5
coupling matrices
Vτ (m)
are combinations of the CG coefficients. Their explicit expressions [we use the shorthand
s
for
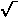 3
and omit the explicit indication of dependence Vhg (m)(α)] are the following: Vgg (-2)=s-1 ( \matrix{ 0
3
and omit the explicit indication of dependence Vhg (m)(α)] are the following: Vgg (-2)=s-1 ( \matrix{ 0
Vhg (-2)=cosα/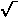 (20) ( \matrix{ 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr s TABsEpArAtOr 0
(20) ( \matrix{ 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr s TABsEpArAtOr 0
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr s TABsEpArAtOr s
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr -1
s TABsEpArAtOr s TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
0 TABsEpArAtOr s TABsEpArAtOr -1 TABsEpArAtOr 0 TABsEpArAtOr 0
} ) + sinα/2 s ( \matrix{ 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 1 TABsEpArAtOr 0
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr -1 TABsEpArAtOr 1
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr s
1 TABsEpArAtOr -1 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
0 TABsEpArAtOr 1 TABsEpArAtOr s TABsEpArAtOr 0 TABsEpArAtOr 0
} ) Vhg (-1)=cosα/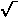 (20) ( \matrix{ 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr s TABsEpArAtOr -s
(20) ( \matrix{ 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr s TABsEpArAtOr -s
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr -s
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 1 TABsEpArAtOr 0
s TABsEpArAtOr 0 TABsEpArAtOr 1 TABsEpArAtOr 0 TABsEpArAtOr 0
-s TABsEpArAtOr -s TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
} ) + sinα/2 s ( \matrix{ 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr -1 TABsEpArAtOr -1
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 1
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr s TABsEpArAtOr 0
-1 TABsEpArAtOr 0 TABsEpArAtOr s TABsEpArAtOr 0 TABsEpArAtOr 0
-1 TABsEpArAtOr 1 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
} ) Vhg (0)=cosα/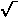 (20) ( \matrix{ 1 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
(20) ( \matrix{ 1 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
0 TABsEpArAtOr 1 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
0 TABsEpArAtOr 0 TABsEpArAtOr -4 TABsEpArAtOr 0 TABsEpArAtOr 0
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 1 TABsEpArAtOr 0
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 1
} ) + sinα/2 ( \matrix{ -1 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
0 TABsEpArAtOr 1 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 1 TABsEpArAtOr 0
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr -1
} ) Vhg (1)=cosα/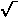 (20) ( \matrix{ -s TABsEpArAtOr s TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
(20) ( \matrix{ -s TABsEpArAtOr s TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
s TABsEpArAtOr 0 TABsEpArAtOr -1 TABsEpArAtOr 0 TABsEpArAtOr 0
0 TABsEpArAtOr -1 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr s
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr s TABsEpArAtOr s
} ) + sinα/2 s ( \matrix{ -1 TABsEpArAtOr -1 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
-1 TABsEpArAtOr 0 TABsEpArAtOr -s TABsEpArAtOr 0 TABsEpArAtOr 0
0 TABsEpArAtOr -s TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr -1
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr -1 TABsEpArAtOr 1
} ) Vhg (2)=cosα/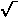 (20) ( \matrix{ 0 TABsEpArAtOr s TABsEpArAtOr 1 TABsEpArAtOr 0 TABsEpArAtOr 0
(20) ( \matrix{ 0 TABsEpArAtOr s TABsEpArAtOr 1 TABsEpArAtOr 0 TABsEpArAtOr 0
s TABsEpArAtOr -s TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
1 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr s TABsEpArAtOr -s
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr -s TABsEpArAtOr 0
} ) + sinα/2 s ( \matrix{ 0 TABsEpArAtOr 1 TABsEpArAtOr -s TABsEpArAtOr 0 TABsEpArAtOr 0
1 TABsEpArAtOr 1 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
-s TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr 0
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr -1 TABsEpArAtOr -1
0 TABsEpArAtOr 0 TABsEpArAtOr 0 TABsEpArAtOr -1 TABsEpArAtOr 0
} ) .
In the static JT effect, the kinetic term in Pτ i m2 is ignored, and the problem is to study the five Born-Oppenheimer (BO) potential sheets given by the sum of each eigenvalue of the electronic problem plus the harmonic restoring forces. The Hu× ag part has a purely diagonal coupling matrix. As it does not split the electronic degeneracy, it is trivially separated from the coupling to the other modes and can be treated as a displaced oscillator.
When a single electron (hole) is placed in the
Hu
orbital, the molecule distorts in such a way that the lowest (highest) BO sheet is lowered (raised) in energy as much as possible. The coupling to a
gg
mode leads to 10 equivalent absolute minima of
D3
local symmetry (Ceulemans and Fowler 1990, Manini and De Los Rios 2000) of the BO potential. The optimal distortion is realized for |qsgg|= ggg/3, with a corresponding potential energy lowering of ggg2 hωgg/18. The
r=2
part of the coupling to the
hg
modes (corresponding to the
sinα
terms in
Vhg (m)
above) contributes to these same minima in an equivalent way, with
ggg
replaced by ghgsinα. However, the
r=1
component (cosα terms in Vhg (m)) of the coupling favours the six classical stable minima of local
D5
symmetry (Ceulemans and Fowler 1990, Manini and De Los Rios 2000). The optimal distortion at these minima is |qshg|= ghgcosα/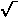 5, for an energy lowering of ghg2
5, for an energy lowering of ghg2 cos2 α hω / 10.
The simultaneous linear coupling to several modes will generally lead to a cumulative distortion and to an energy gain which is the sum of the individual energy gains. However, the form of the coupling (real interaction Hamiltonian) prevents the molecule to gain energy through both kinds of couplings. The system shall choose between a D3 and a D5 distortion, depending which one is energetically more convenient for given specific values of the couplings, vibration frequencies, and Hu orbital electronic filling. The calculation of the following section determines in particular which one of the two types of distortions prevails in C60+.
We compute the molecular electronic structure within the density functional theory (DFT) in the local density approximation. The C60 molecule is repeated periodically in a large fcc supercell lattice. The conventional supercell side is a=18.5 Å, so that the distance between the centers of two neighboring copies of the molecule is 13.1 Å, suitably much larger than the fully relaxed equilibrium (opposite C-C) ball diameter, about 7.053 Å. Since we aim at describing the single molecule -- and indeed our molecules are well isolated -- no sampling of the Brillouin zone is called for, and calculations of the charge density are done using the k=0 wavefunctions. We use ultrasoft pseudopotentials (Vanderbilt 1990) for C (Favot and Dal Corso 1999). The plane-waves basis set is cut off at
Ecut=27
Ry (charge density cutoff = 162 Ry). Test calculations with higher cutoff or larger cell size
a
gave equivalent results.
Based on this electronic structure calculation, we used next density functional perturbation theory (Baroni et al. 1987) to compute three independent rows of the dynamical matrix. Icosahedral symmetry is then used to recover the full matrix, which determines the normal modes \vecξi,s and frequencies ωi (Giannozzi and Baroni 1994) of the molecule. We obtained frequencies (see Table frequencies:tab) in good agreement with experiment (Prassides et al. 1991, Zhou et al. 1992), as well as with previous calculations (Giannozzi and Baroni 1994, Negri et al. 1988, Kohanoff et al. 1992).
| mode | Experim. | Giannozzi & Baroni | this work |
| ag (1) | 496 | 495 | 500 |
| ag (2) | 1470 | 1504 | 1511 |
| hg (1) | 271 | 259 | 261 |
| hg (2) | 437 | 425 | 429 |
| hg (3) | 710 | 711 | 718 |
| hg (4) | 774 | 783 | 784 |
| hg (5) | 1099 | 1120 | 1119 |
| hg (6) | 1250 | 1281 | 1275 |
| hg (7) | 1428 | 1450 | 1456 |
| hg (8) | 1575 | 1578 | 1588 |
| t1u (1) | 527 | 527 | 533 |
| t1u (2) | 576 | 586 | 588 |
| t1u (3) | 1183 | 1218 | 1212 |
| t1u (4) | 1428 | 1462 | 1469 |
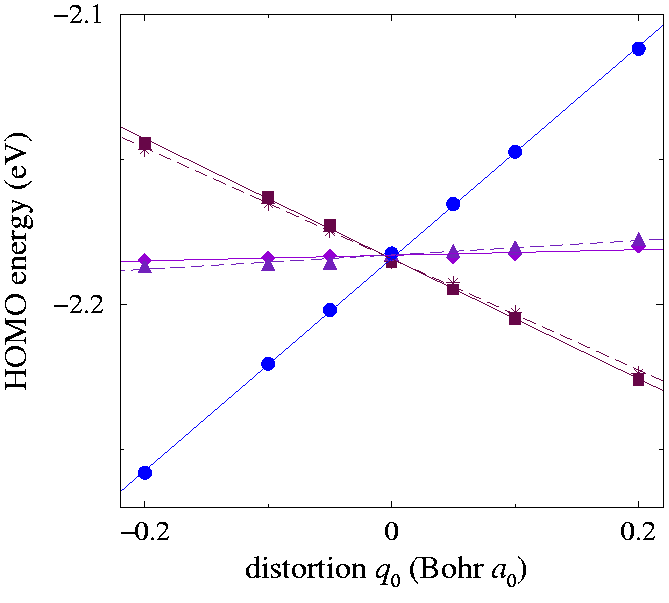
| The splitting of the HOMO degenerate level when the molecule is distorted according to the 6th mode hg (1250 cm-1). Points: DFT data. Lines: linear fits, giving the coupling parameters ghg 6 and αhg 6 of Table couplings:tab. } |
To determine the e-v couplings for the linearly coupled modes, we proceed subsequently to displace the atomic positions from the equilibrium position along each of the normal modes, choosing a suitable eigenvector combination in the linear space of each degenerate vibration. In particular for each hg mode we selected the q0 displacement, corresponding to the totally symmetric combination \vecξi,0 of the distortions \vecξi,s with respect to an (arbitrarily chosen) D5 subgroup of the molecular symmetry group. The five initially degenerate (really, only nearly degenerate, owing to a weak cubic splitting due to the artificial supercell lattice) Hu Kohn-Sham eigenvalues split under this distortion with a pattern given by the eigenvalues of Vhg (0). We applied a displacement of the atomic positions along each of the eight normal-mode unit vectors, \vecξi,0 with a prefactor ranging from -0.1 to 0.1 Å. In Fig. split:fig we plot as an example the resulting energies for the sixth hg mode. The pattern generated by Vhg (0) should be 1+2+2 (a state separated by two pairs of twofold-degenerate states). The small residual splittings of these twofold degeneracies, due to the cubic crystal field and higher-than-linear couplings, give an estimate of the accuracy of the method. By standard linear fitting and comparison with Eq. (real interaction Hamiltonian), we obtained directly the linear dimensionless coupling coefficients ghgi αhgi collected in Table couplings:tab. We determined the sign of αhgi by applying a distortion along \vecξi,1, and comparing the splitting of the HOMO with the eigenvalues of Vhg (1)(± αhgi). Following the same procedure we derived the couplings for the gg modes, by applying here q-1 distortions. The resulting linear coupling coefficients gggi are also collected in Table couplings:tab.
| | coupl. | gτ i | ατ i | qs(D5) | qs(D3)
| Es(D5)
| Es(D3) | \tildeλ \ |
| cm-1 | eV/a0 | deg | a0 | a0 | meV | meV | meV | |
| ag | ||||||||
| 500 | 0.03 | 0.059 | - | 0.00 | 0.00 | 0.0 | 0.0 | 0.1 |
| 1511 | 0.63 | 0.274 | - | 0.01 | 0.01 | 1.8 | 1.8 | 3.5 |
| gg | ||||||||
| 483 | 0.31 | 0.757 | - | - | 0.04 | 0.0 | 1.9 | 8.6 |
| 567 | 0.05 | 0.102 | - | - | 0.00 | 0.0 | 0.0 | 0.2 |
| 772 | 0.67 | 0.800 | - | - | 0.03 | 0.0 | 3.4 | 15.3 |
| 1111 | 0.90 | 0.624 | - | - | 0.02 | 0.0 | 3.0 | 13.4 |
| 1322 | 0.43 | 0.228 | - | - | 0.01 | 0.0 | 0.5 | 2.1 |
| 1519 | 1.08 | 0.467 | - | - | 0.01 | 0.0 | 2.3 | 10.3 |
| hg | ||||||||
| 261 | 0.50 | 3.042 | -0.1 | 0.27 | 0.00 | 30.0 | 0.0 | 75.0 |
| 429 | 0.43 | 1.223 | 30.1 | 0.07 | 0.03 | 6.0 | 1.1 | 19.9 |
| 718 | 0.75 | 0.995 | 89.4 | 0.00 | 0.04 | 0.0 | 4.9 | 22.0 |
| 785 | 0.67 | 0.784 | -2.3 | 0.04 | 0.00 | 6.0 | 0.0 | 15.0 |
| 1119 | 0.32 | 0.221 | 76.6 | 0.00 | 0.01 | 0.0 | 0.4 | 1.7 |
| 1275 | 0.93 | 0.519 | 28.0 | 0.02 | 0.01 | 3.3 | 0.5 | 10.7 |
| 1456 | 2.09 | 0.962 | 28.1 | 0.03 | 0.01 | 13.0 | 2.1 | 41.7 |
| 1588 | 2.15 | 0.869 | -31.1 | 0.03 | 0.01 | 10.9 | 2.2 | 37.1 |
s
and the classical stabilization energies
Es
are tabulated for both
D5
and
D3
distortions and for one hole in the HOMO. The largest total JT energy gain is realized by the
D5
distortions. We also show the contribution of each mode to the resistivity and superconductivity total coupling
\tildeλ=λ/N1(0)
defined in Eq. (M:lambdatransport) [N1(0)= density of states per spin per band at the Fermi level].
For convenience, we also report in Table couplings:tab the amount of optimal JT distortion pertinent to each mode when the HOMO level is occupied by one electron/hole, and the corresponding energy lowering
Es
for both
D5
and
D3
minima. Note in particular the large coupling associated to the lowest
hg
mode, the corresponding distortion leading to an energy lowering practically equal to its quantum hω.
Adding up the JT energy gain of the individual modes, we estimate the total classical potential energy lowering in C60. The
D5
minima gain Es=71 meV, while the
D3
minima gain only Es=22 meV (the contribution of the
ag
modes -- 2 meV -- being included in both cases). It is therefore apparent that the C60+ ion will choose, at least within linear coupling, the
D5
distortion. As was shown in (Manini and De Los Rios 2000), the possibility of a switch to a nondegenerate
Au
dynamical JT GS occurs, for large coupling strength g 6, only under the condition that the
D3
minima are energetically lower or equal to the
D5
minima. This settles finally the issue of the dynamical JT GS symmetry of this molecular ion: it is a regular Berry-phase vibronic state of symmetry Hu, like the parent electronic state (Manini and De Los Rios 2000). No level crossing to a nondegenerate
Au
state is predicted to occur for C60+.
6, only under the condition that the
D3
minima are energetically lower or equal to the
D5
minima. This settles finally the issue of the dynamical JT GS symmetry of this molecular ion: it is a regular Berry-phase vibronic state of symmetry Hu, like the parent electronic state (Manini and De Los Rios 2000). No level crossing to a nondegenerate
Au
state is predicted to occur for C60+.
A static JT coupling resolves the degeneracy of the Hu level: in a distorted configuration it is possible to distinguish individual levels within the HOMO, energy-wise. Figure bandHu5:fig depicts the square modulus of the hole wavefunction for a D5 minimum. The probability density appears to be localized on an equatorial conjugated band, where the poles are the opposite pentagons centered around the D5 axis we chose among the six possible ones.
As a check, with the same method used above to calculate the hole-vibration couplings of the HOMO (Fig. split:fig), we also computed the electron-vibration couplings of the LUMO and obtained the values in Table minus:tab. The total static JT potential energy lowering is 41 meV, of which 3 meV due to the ag modes, and 38 meV due to the hg modes. These values are generally in line with those calculated by previous authors (Antropov et al. 1993, Varma et al. 1991, Lannoo et al. 1991), although there are some differences in the details. Error bars in theoretical determinations of JT couplings of fullerene have proven surprisingly large, possibly reflecting and amplifying errors in the vibrational eigenvectors. Of course as is well known, somewhat larger energy gains are obtained when the true dynamical JT problem, including a full quantum treatment of the vibrons is considered (Auerbach et al. 1994, Manini et al. 1994). We shall leave this calculation in C60n+ for future work.
| | coupl. | gτ i | qs
| Es
| \tildeλ \ |
| cm-1 | eV/a0 | a0 | meV | meV | |
| ag | |||||
| 500 | 0.07 | 0.157 | 0.01 | 0.2 | 0.4 |
| 1511 | 0.78 | 0.340 | 0.01 | 2.7 | 5.4 |
| hg | |||||
| 261 | 0.07 | 0.412 | 0.08 | 2.7 | 13.7 |
| 429 | 0.17 | 0.489 | 0.07 | 6.3 | 31.7 |
| 718 | 0.26 | 0.350 | 0.04 | 5.5 | 27.3 |
| 785 | 0.19 | 0.224 | 0.03 | 2.4 | 12.2 |
| 1119 | 0.28 | 0.193 | 0.02 | 2.6 | 12.9 |
| 1275 | 0.25 | 0.138 | 0.01 | 1.5 | 7.6 |
| 1456 | 0.69 | 0.315 | 0.03 | 9.0 | 44.8 |
| 1588 | 0.72 | 0.289 | 0.02 | 8.2 | 41.2 |
s, the classical stabilization energies Es, and the contribution to \tildeλ=λ/N1[0].
When more than one electron/hole occupies the HOMO of C60, larger distortions and more important energy gains are expected. In particular, the ag contribution for C60n+ is simply:
which can become as large as 179 meV for
n=10
holes. Consider now the nontrivial JT part of the coupling, that to
gg
and
hg
modes. For
n=2
electrons/holes (spin singlet configuration) in the HOMO orbital, the distortions simply become twice as large as in the
n=1
case, with JT energy gains which are four times larger. Even though
n=1,2
electrons/holes take advantage only of the
D5
stabilization energy, additional electrons/holes can benefit from the extra HOMO splitting induced by the hg(r=2) plus
gg
coupling. To test this, we relaxed completely the molecular structure in the 64-dimensional space of the 8
hg
and
gg
modes, and determined the minima of the total potential energy, filling the five BO sheets as drawn in the insets of Fig. eclassn:fig. For simplicity we only considered at this stage low-spin configurations, generally the most favored by JT. The resulting energy gains
Esgg+hg(n)
are reported in Fig. eclassn:fig. The energy lowering is maximum for
n=4
(and n=6): it is as large as 401 meV, compared to a modest Eshg(n=2,4)=153 meV in C60-. Similarly to what happens in the
T1u
LUMO case (see Fig. eclassn:fig and Manini et al. 1994), the half-filled configuration
n=5
is slightly unfavorable (by JT energetics) with respect to the neighboring
n=4
and
n=6
states. We find that the contributions of the
gg
modes, strictly zero for n=1,2, are small (~ 1 meV) but nonzero in the
3 n
n 7
configurations. This indicates that for such large fillings the many-modes JT system (Manini and Tosatti 1998) can take some advantage also of the ``losing''
gg
+
hg(r=2)
part of the coupling (favoring
D3
minima for n=1,2). The insets of Fig. eclassn:fig, indicate that the largest displacement of a single level in the
Hu
HOMO, about 0.28 eV, is realized for n=2. Finally, we have particle-hole symmetry E
7
configurations. This indicates that for such large fillings the many-modes JT system (Manini and Tosatti 1998) can take some advantage also of the ``losing''
gg
+
hg(r=2)
part of the coupling (favoring
D3
minima for n=1,2). The insets of Fig. eclassn:fig, indicate that the largest displacement of a single level in the
Hu
HOMO, about 0.28 eV, is realized for n=2. Finally, we have particle-hole symmetry Esgg+hg(n)=Esgg+hg(10-n), at an opposite minimum distortion \vec qs(n)=-\vec qs(10-n). For the special case
n=5
this means that the configuration drawn in the inset and the one obtained reflecting the 5 levels through zero give both the same optimal energy (at opposite distortions).
Application of the above results to real C60n+ must await the inclusion of electron-electron Coulomb repulsion. Coulomb interactions will generally compete with JT coupling and favor high-spin configurations, which, in turn, are generally less favorable for JT. (For example for n=2 the triplet configurations has a JT gain of 100 meV instead of 277 meV for the singlet.) We shall return to a more detailed description of C60n+ ions in later work.
In order to relate the previously calculated electron-vibron coupling constants to relevant solid state physical quantities, we start by re-deriving its contribution to the transport relaxation time. We are interested in particular to the features of an orbitally degenerate band as in the charged C60 case. The Boltzmann equation in the presence of a uniform and static electric field \vec{E} reads
e\vec{v}kµ· \vec{E}  n0(εkµ)/
n0(εkµ)/ εkµ = (
εkµ = ( nk,µ/
nk,µ/ t)coll.
t)coll.
being
nk,µ
and
εkµ
the occupation number and energy at momentum
k
for orbital µ, and \vec{v}kµ=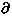 εkµ/
εkµ/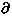 \vec{k}.
\vec{k}.
Within the relaxation time approximation,
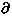 nk,µ/
nk,µ/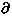 t = δ nk,µ/τkµ
so that the variation with respect to equilibrium becomes
t = δ nk,µ/τkµ
so that the variation with respect to equilibrium becomes
δ nk,µ = - 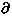 n0(εkµ)/
n0(εkµ)/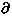 εkµ e \vec{v}kµ· \vec{E} τkµ,
εkµ e \vec{v}kµ· \vec{E} τkµ,
and the conductivity is obtained in the form
σ = -e21/3VΣkµ τkµ \vec{v}kµ · \vec{v}kµ 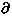 n0(εkµ)/
n0(εkµ)/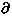 εkµ,
εkµ,
V being the volume, measured in cell units.
As is usual in the treatment of different scattering mechanisms within Fermi's golden rule approximation, one has to sum the inverse of the corresponding relaxation times. The collision term due to the electron-vibron coupling is given, within Fermi's golden rule, by
Here Nτ iq,m is the Bose-Einstein occupation number of phonons of crystal momentum q, symmetry τ = ag,gg,hg, mode i, component m. nk,µ is the Fermi occupation of HOMO band component µ=-2,...,2 at the given temperature and chemical potential. At equilibrium, the collision term is zero. We expand to first order in the deviation from equilibrium.
First, let us consider the case
T>> Maxi(hωi)
but still
T<< TF
(the Fermi temperature). In this case
Nτ iq,m  k
kB T/hωτ i >> 1,
and
&( 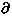 nk,µ/
nk,µ/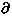 t)coll = - 2π/
t)coll = - 2π/h1/2 V Σp Σi,τ,m,ν (gτ ihωτ i/2)2 | Vτ(m)νµ(ατ i)|2 kB T/hωτ i {\phantom{Σab} .
& (δ nk,µ-δ np,ν) [ δ(εkµ -εpν - hωτ i) + δ(εkµ -εpν + hωτ i)\right]}.
Since T>> Maxi(hωi), after inserting (M:relaxation time approximation) into (M:collision term final) and using the Boltzmann equation, we find that
1/τkµ = 2π/ h1/2 V Σp Σi,τ,m,ν (gτ ihωτ i/2)2 | Vτ(m)νµ(ατ i)|2 kB T/hωτ i {\phantom{Σab} .
& (1-\vec{v/<SUB>pν·\vec{n}} {\vec{v}kµ·\vec{n}}) [ δ(εkµ -εpν - hωτ i) + δ(εkµ -εpν + hωτ i)\right]},
If we approximately take εkµ=εk we find, since the electron-vibron matrices are symmetrical,
1/τk = π/ h Σi,τ,m, (gτ ihωτ i/2)2 Tr[\left(Vτ)2]/d kB T/hωτ i {\phantom{Σab} .
& 1/VΣp (1-\vec{v/<SUB>p·\vec{n}} {\vec{v}k·\vec{n}}) [ δ(εk -εp - hωτ i) + δ(εk -εp + hωτ i)\right]} .
\tildeλ = Σi,τ,m gτ i2 hωτ i/4 Tr [\left(Vτ)2]/d ,
related to the conventional dimensionless ep-phonon coupling λ by
where N1(εF) is the density of states per spin per band at the Fermi energy.
By using Eq. (M:lambdatransport) and the calculated e-v coupling parameters of Table couplings:tab, we find for holes in the Hu HOMO-derived band
This value can be compared with that calculated similarly, using our couplings of Table minus:tab for electrons in the T1u band
We conclude therefore that holes have a stronger scattering with intra-molecular optical phonons than electrons, by about a factor 1.4.
To confirm the accuracy of the values computed for the HOMO case, it is useful to compare those for the LUMO with previous similar calculations. It is then necessary to take into account the factor d=3 which is usually incorporated in the total density of states (Lannoo et al. 1991). Our \tildeλ/d=66 meV compares well with previous similar calculations for the C60 LUMO (Antropov et al. 1993, Varma et al. 1991, Lannoo et al. 1991), ranging from 49 to 68 meV. On the other hand, empirical estimates based on a fit to photoemission data tend to give a value as large as 147 meV (Gunnarsson et al. 1995). The origin of this discrepancy is presently unclear.
The dimensionless electron-vibron coupling which governs the transport properties, λ of Eqs. (M:lambdatransport,lambdadef:eq), is not in point of principle coincident with the parameter λ determining the superconducting properties. The latter must be determined by solving the Migdal-Eliashberg equation with the retarded interaction mediated by the vibrons plus the electron-electron Coulomb repulsion. However, a simple estimate of the order of magnitude of λ can be obtained by taking the unretarded limit, and imposing a Debye cutoff to the electron energies. We assume the electronic band operators to be related to the molecular creation and annihilation operators through the unitary (orthogonal) transformation cnkσ = U-1nµ(k) dµ k σ, n being the band index, σ the spin. Let us define a matrix W by
Wµν = Στ,i,\widehat m gτ i2 hωτ i/4 (Vτ(\widehat m)µν)2 = Στ Wτµν Σi=1nm(τ) gτ i2 hωτ i/4,
as well as
Wnk,mp = Στ,i,\widehat m Σµ1,µ2,µ3,µ4 gτ i2 hωτ i/4 U-1nµ1(k) Vτ(\widehat m)µ1µ2 Uµ2 m(-p) Uµ3 m(p) Vτ(\widehat m)µ4µ3 U-1nµ4(-k),
The Bardeen-Cooper-Schrieffer (BCS) gap equation for
Δk,n = < c+k, ,nc
,nc+-k,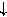 ,n >,
reads
,n >,
reads
Δk,n = 1/2VΣp,m Wnk,mp Δp,m/Ep,m tanh(βEp,m/2),
where
Ep,m=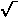 ((εpm-µ0)2 + Δp,m2),
µ0
being the chemical potential. The critical temperature is obtained by solving the eigenvalue equation
δnmδkp - 1/2VΣp,m
((εpm-µ0)2 + Δp,m2),
µ0
being the chemical potential. The critical temperature is obtained by solving the eigenvalue equation
δnmδkp - 1/2VΣp,m Wnk,mp 1/|εpm-µ0| tanh(βc|εpm-µ0|/2) = 0.
In general, the BCS gap equation (M:BCSeq) leads to interference between the Cooper pairs belonging to different bands. That, in turn, increases the critical temperature relative to a situation in which the pairs do not interfere. We may therefore foresee two opposite limits of strongly interfering and of non interfering pairs which, respectively, over and underestimate the effective coupling strength λ.
If we assume that averages over the Fermi surface do not depend on the band indices (interfering pairs, corresponding, for example, to the choice of Lannoo et al. 1991), then we can replace
W
with W, and we find that the critical temperature is determined by the maximum eigenvalue of the matrix
W
in Eq. (M:W). Under this assumption, the superconducting
λ
is determined through
For our H × (a+g+h) e-ph coupling the matrices Wτ are:
Wgg=1/24 \pmatrix{ 8
Whg = 1/60 \pmatrix{ 16 14 9 14 7
14 16 9 7 14
9 9 24 9 9
14 7 9 16 14
7 14 9 14 16
}
&+ cos(2 α)/30 \pmatrix{ -2 2 -3 2 1
2 -2 -3 1 2
-3 -3 12 -3 -3
2 1 -3 -2 2
1 2 -3 2 -2
}
&+ sin(2 α)/4 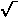 5 \pmatrix{ 0
5 \pmatrix{ 0 0 -1 0 1
0 0 1 -1 0
-1 1 0 1 -1
0 -1 1 0 0
1 0 -1 0 0
} ,
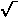 5
is an eigenstate of each of them. Moreover, for each
τ
this eigenstate provides the largest eigenvalue
5
is an eigenstate of each of them. Moreover, for each
τ
this eigenstate provides the largest eigenvalue
Maxeigenvalue(Wτ)=Σn Wτmn=1
(for any m and τ). This means that the totally-symmetric paired state, delocalized over all the five Hu orbitals or bands, is favored by the couplings to all modes. It also implies that, contrary to molecular JT, the couplings to all modes cooperate evenly to this superconducting state, and contribute additively to λ. Totally equivalent (even if at first sight apparently different) results were derived for the d=3 case (K3C60) in Refs. (Lannoo et al. 1991, Rice et al. 1991). We note, however, that the claim that orbital degeneracy enhances the superconducting λ through a factor d (Rice et al. 1991) is not really justified, as one must at the same time reduce the density of states from total to single-band, a factor 1/d smaller. We also note that
1= Σn Wτmn= Σmn Wτmn/d= Σmn VτmnVτnm/d= Σm [(Vτ)2]mm/d = Tr[(Vτ)2]/d ,
which shows the identity of the \tildeλ computed for superconductivity to the one obtained for transport in Eq. (M:lambdatransport).
If, in the opposite limit, the pairs did not interfere between different bands, the effective λ would be reduced by a factor d. Although we cannot identify a physical situation corresponding to this limit, we can assume that a general case will be intermediate between the limits (interfering/not-interfering pairs). For simplicity, we will stick here to the interfering limit.
In summary, is there any enhancement of superconductivity due to orbital degeneracy? We can still identify one possible source for that, namely Coulomb pseudopotential. In fact, we note that, although a large λ due to tunneling of the Cooper pairs between different orbitals/bands, can be seen as orbital degeneracy enhancing the effective λ to the highest eigenvalue of W, there is no corresponding enhancement of the repulsive Coulomb pseudo-potential µ*, at least within the Migdal-Eliashberg theory. The reason is that the main contribution to the Coulomb pseudo-potential is a charge-charge repulsion which does not include tunneling processes between different bands, and being band-diagonal it does not get enhanced. In conclusion, in the above restricted sense, orbital degeneracy may in principle favor superconductivity.
We have presented a density functional calculation of the linear coupling of holes/electrons in the Hu and T1u orbitals of the fullerene molecule to the intra-molecular vibrations. The coupling to holes is strongest for the hg modes, and among those to the lowest-frequency mode hg(1) around 270 cm-1. The linear static Jahn Teller distortion predicted for C60+ by these couplings corresponds to a D5 distortion, with an energy gain of 71 meV.
The corresponding dynamical JT state expected with the calculated coupling parameters is a regular Berry-phase vibronic state of symmetry Hu, like the parent electronic state (Manini and De Los Rios 2000). There is no level crossing to a nondegenerate Au state, as would have hypothetically been possible on pure symmetry grounds, had the D3 minima been the stable ones (Manini and De Los Rios 2000).
In order to connect with important solid state properties including transport and superconductivity we have formulated a theory of the Boltzmann relaxation time, and of the BCS-type pairing, suitable for an orbitally degenerate multiband case with Jahn Teller coupling. This confirms that the same parameter λ determines both transport and superconducting properties of the multiband degenerate solid. As we previously observed, not all the computed gi (Table couplings:tab) are small parameters, and thus weak-coupling BCS theory is strictly not applicable for C60n+. However, the overall λ is still moderate. Our calculation neglects couplings to acoustic phonons and librations, which in principle should also contribute to e-ph scattering. In addition, similarly to Lannoo et al.'s calculation (Lannoo et al. 1991), we assume that the dispersion of the HOMO band and of the optical phonons has a negligible effect on the integrated value of λ. (This assumption was tested and proved correct in Ref. (Antropov et al. 1993) for the couplings to the LUMO band.) With all these approximations, Eq. (M:lambda) should provide a semi-quantitative estimate of the total e-ph scattering.
Assuming conservatively a total average density of states of ~ 10/0.6 eV~17 states eV-1 for the HOMO band (i.e. a single-band density of states
N1(0)
= 1.7 states eV-1 per band per spin), our calculated effective dimensionless
λ+
for hole superconductivity in C60 is in conclusion about λ+~0.47. The Coulomb pseudopotential
µ*
is not available yet, but possibly in the same range of values as for negative C60 [µ*~ 0.2÷ 0.3 (Gunnarsson et al. 1995, Gunnarsson and Zwicknagl 1992)]. With this value of λ+, weak coupling would predict Tc ~ 1.14 hωD kB-1 exp[-1/(λ+ -µ*)]~ 40 K for µ*= 0.2, and Tc~ 5 K for
µ*= 0.3
(assuming a typical phonon energy
ωD
of about 1500 K). This seems of the correct order of magnitude, although somewhat on the low side, in comparison with Tc= 52 K found experimentally. However, it is difficult to justify weak coupling in this case.
The corresponding value λ- which we obtain for electrons in the T1u orbitals is, assuming the same bandwidth of 0.6 eV, thus again N1(0) = 1.7 states eV-1 per band per spin for the T1u band, λ-~ 0.33. The factor λ+/λ-=1.4 of holes relative to electrons is in qualitative agreement with a larger Tc of the former. Assuming the same typical phonon frequency, BCS would predict here Tc~ 0.8 K for µ*= 0.2, and Tc~ 0 K for µ*= 0.3. That is obviously way smaller than the observed superconducting Tc= 10 K found experimentally in the field emission transistor (FET) experiment, let alone the higher values found in the fullerides.
Coming to transport, the measured resistivities for holes are larger than those of electrons, and this also agrees with a larger λ value. Calculation of the T-linear high temperature resistivity ρ = λtr T/4πωp2 would however predict a moderately larger value for hole- than for electron-doped C60, at least assuming (somewhat arbitrarily) the same plasma frequencies for the same carrier densities. Quantitatively, Batlogg's FET data (Schön et al. 2000) differ strongly from this expectation. They, first of all, indicate a nonlinear temperature dependence, closer to T2; secondly, they show values about 5 times larger for holes than for electrons. While there are second order processes (see Appendix) that would indeed yield a T2 resistivity at low temperatures, we do not believe that they may explain the discrepancy here. Zettl and coworkers (Vareka and Zettl 1994) proposed that the apparent T2 in the electron resistivity is an effect of thermal expansion, and showed that a linear T increase is recovered at constant volume, for negative doping.
Recently Goldoni et al. measured by EELS the plasma frequency in K3C60. They found it slowly decreasing with temperature, its width growing approximately quadratically with T. These data support the view that the T2 resistivity is directly related with a T-2 decrease of relaxation time, most likely linked with lattice expansion. It seems plausible that a similar physics could apply to holes too, in which case the predicted constant-pressure relaxation-time drop with temperature would also be non-linear, and quantitatively larger than the electron case. If, on the other hand, it became possible to obtain the constant-volume inverse relaxation time and resistivity, then, assuming the same plasma frequency ωp, its increase should be linear with T with a slope 1.4 times larger than that of negatively-charged C60. This conjecture must await experimental test.
We are indebted to B. Batlogg, O. Gunnarsson and G. Santoro for useful discussions. This work was partly supported by the European Union, contract ERBFMRXCT970155 (TMR Fulprop), and by MURST COFIN99.
Within Fermi's golden rule, the vibron contribution to the electrical resistivity is exponentially decreasing if temperature is much smaller than the vibron frequencies. However, the above result is not true any more if higher order corrections are taken into account. Indeed, at second order, the electron-vibron coupling generates an effective electron-electron interaction. Since the electrons involved lie on a shell of width T around the Fermi energy, the vibron-originated electron-electron interaction
Vel-el(ω) = - Στ,i,m gτ i2 hωτ i/4 ωτ i2/ωτ i2 - ω2
&1/VΣkpqΣµνγβΣσ,σ' Vτ(m)µν(α) Vτ(m)γβ(α) d +µ,σ,k+q d+γ,σ',p dβ,σ',p+q dν,σ,k ,
1/τ ~ (k B T)2/5h N1(εF)3 Σi,j,τ,τ',m,m' (gτ i2 hωτ i/4) (gτ' j2 hωτ' j/4)
& { 5/4 [ Tr(Vτ(m)Vτ'(m'))\right]2 - Tr( Vτ(m)Vτ'(m')Vτ(m)Vτ'(m')) } .
Automatically converted from LaTeX by convert2html v. 3.21 [24 URL-ed refs]
| created: 20 Aug 2002 | last modified: 20 August 2002 by Nicola Manini |