Phonons of a 1D chain

In the adiabatic framework, we study the normal modes of a linear chain of atoms assumed to be allowed to displace only along the chain, not perpendicularly to it. Take 2 N equal atoms, represented by classical point particles, assume they are bound to sit in a line, and assume their lowest-energy configuration is a regular arrangement with two of them per unit cell. (Here one has in mind a molecular crystal, e.g. made of O₂ or N₂ or Cl₂ units. It is a very unrealistic model, as it would be very hard to convince such molecules to crystallize along a line!)

Call u_{1 j} and u_{2 j} the displacements from equilibrium of the left and right atom respectively of the j-th cell. To search for the normal modes of oscillations, the adiabatic potential energy of the lattice must be expanded to lowest (quadratic) order in the displacements from equilibrium. In the approximation that each atom is affected only by its nearest neighbors we write the potential energy as a function of the displacements as:

U = U₀ + K/2 ∑_j (u_{1 j} - u_{2 j})² + G/2 ∑_j (u_{2 j} - u_{1 (j+1)})²

where K and G are the "force constants" characterizing the curvature of the nearest neighbor 2-body potential at the equilibrium point, and U₀ is the total binding energy of the crystal at equilibrium (irrelevant for our purposes). The sums over j are extended to the N cells of the lattice, assuming, for simplicity, periodic boundary conditions, i.e. when an index takes a value N+1 it is meant to be 1, and when it takes a value 0 it means N.

Newton's equations of motion for the harmonic oscillations are:

m d²u_{1 j}/dt² = -∂U/∂u_{1 j} = - K (u_{1 j} - u_{2 j}) - G (u_{1 j} - u_{2 (j-1)})
m d²u_{2 j}/dt² = -∂U/∂u_{2 j} = - K (u_{2 j} - u_{1 j}) - G (u_{2 j} - u_{1 (j+1)})

The normal modes are characterized by an oscillatory behavior. The symmetry of the crystal makes us take a wave form for the normal displacements:

u_{1 j} = ε₁ exp[i (k j a - ω t)]
u_{2 j} = ε₂ exp[i (k j a - ω t)]

where a is the lattice parameter (in practice the length of the unit cell).

Note that any phase difference between atoms in the cell is taken care by the relative phase of ε₁ and ε₂, while phase differences between different cells are governed by the exp[i k j a] common factor. By plugging this wavy solution into Newton's equation of motion, one gets the secular equation for the normal modes. Note that the "trick" of using translational invariance has reduced the 2N×2N secular problem to a simple 2×2 problem, with a parametric dependence on k.

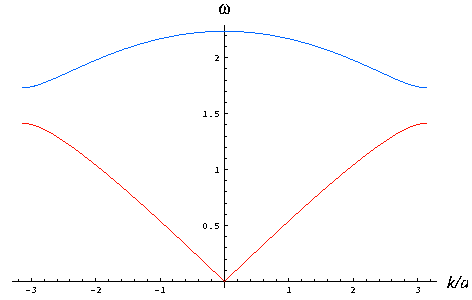
The resulting normal frequencies are:

ω_+/-(k) = [(K + G ± |K + G e^{i k a}|)/m]^½

These normal frequencies are plotted at the right as a function of k in the first Brillouin zone (for m=1, G=1, K=1.5). The upper curve ω₊(k) traces the optical branch (blue) of the phonon dispersion. The lower curve ω_-(k) represents the acoustic branch (red). The plot (or rather a power expansion around k=0) makes it clear that the optical branch has a (constant - k²) behavior, while the acoustic branch is characterized by a photon-like linear dispersion |k| at small k. The special normal mode at ω_-(0) = 0 represents an infinite-wavelength "oscillation", in practice the translation mode of the whole crystal: due to translational invariance of U, it has 0 frequency.

The k variable changes continuously in the (-π/a,π/a] interval only in the limit of a chain composed by an infinite number of particles. For finite N, only N equally spaced k values are allowed in the first Brillouin zone.

The eigenvectors of the secular problem describe in detail the motion of the atoms for each k and branch. One gets:

ε₂^± / ε₁^± = ^-₊ (K + G e^{i k a})/|K + G e^{i k a}| .

Exercises

Evaluate the dispersion and normal-mode displacements in the simpler case of atoms and bonds of one kind (K=G, one atom per unit cell, N atoms). Afterwards, you may check the solution.
Draw explicitly the oscillation modes as small arrows on top of each atom for:
- small k, the acoustic branch;
- small k, the optical branch;
- k close to zone boundary π/a, the acoustic branch;
- k close to zone boundary π/a, the optical branch;
Study in detail the limiting case G << K. Show in particular that the acoustic branch is equivalent to oscillations of point particles of mass 2m, connected by springs of constant G. What does the optical branch represent instead?
Study the case of two different masses m₁, m₂ at the two lattice sites. [The hypothetical crystal one has in mind is either made up of molecules such as HCl for example (different G and K), or a 1-dimensional NaCl ionic crystal (K=G)]
RESULT: ω_±² = (K + G)/(2µ) (1 ± [1 - 16µ/(m₁+m₂)KG/(K + G)² sin²(ka/2)]^½), with µ=m₁m₂/(m₁+m₂).
Write down explicitly the 3×3 dynamical matrix for the simpler problem of the 1-dimensional motions of a linear molecule such as CO₂. Find the normal-mode frequencies and eigen-vibrations in the same approximation used above, namely that the force on each O depends only on its distance to the central C atom and not on the position of the other O atom.

Notes

The normal modes we found are not the only possible motions a harmonic system can follow, quite the contrary! The general motion will be a superposition of the harmonic motions of different frequencies, which is non-periodic, in general.
Of course, in our 3D world there is no such a thing as a 1D crystal. Even such a linear chain-like object as a polymer, has transverse degrees of freedom in addition to the longitudinal ones we treated here. As a result, an actual crystal would have 3 phonon branches per atom in the unit cell, instead of 1. Our 1D description is quantitatively adequate for the longitudinal vibrations along a crystal symmetry axis.
The amount of excitation of each normal mode is not affecting in any way all the other modes' frequencies and amplitudes. This is a consequence of the linearity of the classical equations of motion, a consequence of the harmonic approximation.
Of course, in reality there is no such a thing as a harmonic crystal (or molecule)! The normal-mode decomposition is an useful toy model to understand the nature of the characteristic frequencies in the limit of infinitely small oscillations. However, in practice all classical oscillations have finite amplitude (see also next point), and they are therefore bound to interact due to anharmonicity. The frequency of some mode does depend on the amount of excitation of another one ...
There is no such a thing as a classical crystal. We have used Newton's equations of motions here, but clearly the atomic movements follow Schroedinger's equation, not Newton's. A standard "trick" is to use the classical normal-mode displacements as coordinates for the subsequent quantization. In these coordinates, representing collective displacements of all the atoms in the lattice, the Hamiltonian is separated in a sum of independent harmonic oscillators (a standard problem in quantum mechanics), plus the non-harmonic interaction terms. The harmonic part is very similar to that of the electromagnetic fields in a box (the photons): for analogy, the quanta of these oscillators are called the phonons. The main difference between the two cases is that while the photons are exactly non-interacting, higher-order non-harmonic corrections to the potential make phonons interact (decay, recombine....). The quantum wavefunction explores all the phonon coordinate range, it is not bound to remain close to the minimum. In particular even in the quantum ground state there is a finite amount of zero-point motion: therefore a quantum crystal cannot be confined to "small" oscillations, in the region where the quadratic potential is a good approximation. Anharmonic effects are always present. Luckily, for heavy rigidly bound covalent crystals at not too high temperatures non-harmonic effects are fairly small, and the harmonic crystal model compares fairly well to experimental data (for example, measured specific heat).
More infos on inelastic neutron scattering: the standard technique to investigate phonon dispersion experimentally.

created: 17 Jan 2002

last modified: 5 Nov 2021

by Nicola Manini