STRUTTURA DELLA MATERIA -- 18 settembre 2003
home |
group |

|
![[separation line]](http://materia.fisica.unimi.it/manini/images/line.colorbar.gif)
- laurea quadriennale:
la soluzione corretta di 3 esercizi garantisce l'ammissione all'esame orale;
- laurea triennale:
la soluzione corretta di 2 esercizi garantisce l'ammissione all'esame orale;
- avvertenza:
si giustifichino con poche parole tutti i passaggi; verranno considerate nulle le soluzioni anche giuste prive delle corrette giustificazioni.
-
Determinare la massa a riposo persa dal sole ogni secondo per emissione di radiazione. Assumere che la temperatura del sole sia 5700 K e il diametro 1.4× 109 m. Qual'è la frazione di massa persa ogni anno se l'attuale massa a riposo del sole è pari a 2× 1030 kg.
[Esclusi studenti laurea triennale]
-
Si trascuri la probabilità che atomi di bromo gassoso a 500 K occupino stati diversi da [Ar]3d104p5 2P3/2. Accendendo un campo magnetico uniforme la degenerazione delle componenti di questo multipletto è risolta: quale sarebbe l'intensità di tale campo necessaria a stabilire una popolazione d'equilibrio uguale per lo stato fondamentale e per il totale delle componenti eccitate? [Suggerimento: la radice dell'equazione
cosh(x)=sinh(3x)
è x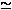 0.304689]
0.304689]
-
Dati i seguenti valori misurati di calore specifico del diamante, si determini la sua temperatura di Debye:
| T
[K] | CV
[J K-1 Kg-1]
|
| 10 | 0.0146
|
| 20 | 0.117
|
| 100 | 14.6
|
| 300 | 344
|
} [Si ricorda l'espressione per l'energia interna vibrazionale molare nel modello di Debye: U = 9 R T4/ΘD3 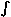 0ΘD/T x3 dx/ex -1
0ΘD/T x3 dx/ex -1 e che 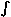 0
0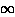 x3 dx/ex -1 = π4/15 ]
x3 dx/ex -1 = π4/15 ]
-
L'energia di legame
E(R)
di una molecola di Na2 in funzione della distanza
R
tra gli atomi può essere rappresentata dalla forma (di Morse):
E(R)= Eb [ e-2a(R-R0) - 2 e-a(R-R0) ]
con
Eb=0.75
eV, R0=3.07 Å e a=0.84 Å-1. Determinare la distanza di equilibrio e l'energia di legame della molecola Na2, la frequenza delle piccole oscillazioni e il suo momento di inerzia. Con questi dati valutare il rapporto tra il numero di molecole nel primo livello eccitato e il numero di molecole nello stato fondamentale a T=300 K sia per le eccitazioni rotazionali che per quelle vibrazionali.
-
Le linee spettrali della transizione 3p--->3s del sodio hanno lunghezze d'onda λ1=5889.6 Å e λ2=5895.9 Å. Supponendo di applicare a dei vapori di sodio un campo magnetico esterno che dia luogo a effetto Zeeman, si valuti l'intensità di tale campo affinché le linee (di dipolo elettrico) che si avvicinano maggiormente si portino al 90% della separazione energetica che avevano in assenza di campo.
Segue una lista di valori comunemente accettati per alcune costanti fisiche rilevanti:
c=299792458 m/s, h=1.05457267· 10-34 J s, e=1.60217733· 10-19 C, e2/(4 π ε0) = 2.30707956· 10-28 J m, me=9.1093897· 10-31 kg, mp=1.6726231· 10-27 kg, a.m.u.=1.6605402· 10-27 kg, kB=1.380658· 10-23 J/K, NA=6.0221367· 1023 mol-1.
Automatically converted from LaTeX by convert2html v. 3.29 [0 URL-ed refs]
| version date: 19 Sep 2003 |
date conversion: 19
September
2003
by
Nicola Manini |


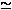 0.304689]
0.304689]
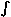 0ΘD/T x3 dx/ex -1
0ΘD/T x3 dx/ex -1 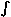 0
0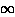 x3 dx/ex -1 = π4/15 ]
x3 dx/ex -1 = π4/15 ]