STRUTTURA DELLA MATERIA 1 -- 20 settembre 2023

• Almeno 2 problemi risolti correttamente garantiscono l'ammissione all'esame orale.
• Avvertenza: si giustifichino con poche parole tutti i passaggi; verranno considerate nulle le soluzioni anche corrette prive di adeguate giustificazioni.

1. Il pattern di diffrazione di un campione di silicio cristallino mostra un picco all'angolo di Bragg θ=75.00^° alla temperatura di 290 K, che si sposta all'angolo θ=74.50^° quando si porta il campione alla temperatura di 1200 K. Si calcoli il coefficiente di dilatazione termica lineare del silicio. [Si ricorda che il coefficiente di dilatazione termica è definito come 1/l   (Δ l)/(Δ T), e si misura in K^-1. In questa definizione si ponga l=[l(T₁)+l(T₂)]/2.]

2. Si consideri un cristallo monodimensionale con passo reticolare a=330 pm nel quale ciascun sito del reticolo è occupato da un atomo di berllio (Z=4). Gli elettroni di valenza (2 per atomo) possono occupare le seguenti due bande: ε^a_k=-t  cos(ka)  ,     ε^b_k=t'   cos(ka) +Δ  . Per le due scelte dei parametri (i) t=1 eV, t'=0.3 eV, Δ=1.5 eV e (ii) t=2 eV, t'=1 eV, Δ=1.5 eV si verifichi se il solido è un metallo un isolante o un semiconduttore, e se ne determini l'energia di Fermi a T=0. Nel caso di un solido isolante o semiconduttore, si valuti la massa efficace di eventuali elettroni eccitati nel fondo della banda di conduzione, e la si esprima in unità della massa dell'elettrone nel vuoto.

3. L'energia di prima ionizzazione dell'atomo di boro risulta pari a 8.3 eV. Sono osservate linee spettrali alle lunghezze d'onda elettromagnetiche riportate nel grafico: 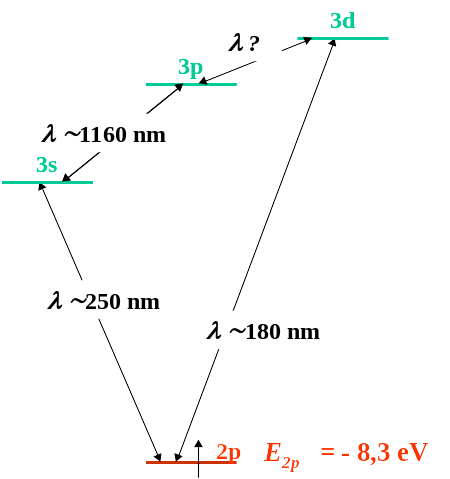Utilizzando i dati indicati, si calcolino le energie dei livelli eccitati 3s, 3p e 3d riferite al livello d'energia del monocatione B⁺ preso convenzionalmente come zero, e la lunghezza d'onda della transizione 3d→3p.

4. L'identità degli atomi componenti la molecola H₂ impone che, nel ket globale, il fattore che descrive lo spin nucleare e quello che descrive il moto adiabatico rotovibrazionale abbiano la stessa parità per scambio dei due atomi; dunque: I_tot=0 implica L pari (paraidrogeno) e I_tot=1 implica L dispari (ortoidrogeno). Data la temperatura rotazionale θ_rot = 87 K, si valuti la frazione d'equilibrio di paraidrogeno sul totale a T=400 K e a T=θ_rot.

Segue una lista di valori comunemente accettati per alcune costanti fisiche rilevanti:
c=299792458 m/s, ℏ=1.0545718⋅ 10^-34 J s, q_e=1.6021766⋅ 10^-19 C, e² = q_e²/(4 π ε₀) = 2.3070776⋅ 10^-28 J m, m_e=9.109384⋅ 10^-31 kg, m_p=1.672622⋅ 10^-27 kg, m_n=1.674927⋅ 10^-27 kg, a.m.u.=1.660539⋅ 10^-27 kg, k_B=1.380649⋅ 10^-23 J/K, N_A=6.022141⋅ 10²³ mol^-1.