Sensitivity of the Mott transition to noncubic splitting of the orbital degeneracy: Application to NH3K3C60
home | group
Sensitivity of the Mott transition to noncubic splitting of the orbital degeneracy: Application to NH3K3C60home | group |

|
21-08-2002
Strong electron correlations in multiband, orbitally degenerate systems represent an important current theoretical challenge. A lively experimental playground for that is provided by electron- and hole-doped fullerene systems, which exhibit a variety of behavior, including unconventional metals like cubic CsC60[Brouet99], superconductors of the A3C60 family (A= K,Rb,Cs)[Ramirez][Gunnarsson97], superconducting field-effect transistor (FET) devices[schon00][Batlogg00], and insulators, presumably of the Mott-Jahn-Teller type[Fabrizio97][Capone00]. Among them we can place A4C60 [Benning], Na2C60[Brouet01] and the class of compounds NH3K3C60, NH3K2RbC60, NH3KRb2C60, and NH3Rb3C60[Rosseinsky93][Takenobu00][Obu00]. In these ammoniated compounds, insertion of the electronically inert NH3 molecules acts to expand the C60 lattice, turning the cubic, metallic, and superconducting state of K3C60 into an orthorhombic narrow-gap antiferromagnetic insulator [Rosseinsky93][Takenobu00][Tou1]. In this transition, the increase in volume per C60 molecule relative to K3C60, with its probable slight decrease of electron effective bandwidth W, is believed to play an important role, as confirmed by the pressure-induced reversion to a fully metallic and superconducting -- while still orthorhombic -- phase [Zhou95][Margadonna01].
Nonetheless, a possible role of the crystal-structure anisotropy in this Mott transition -- a transition generally believed to occur more readily for reduced orbital degeneracy[Gunnarsson96][Koch99], cannot be excluded. It has even been proposed that precisely the splitting of degeneracy[splitting:note] induced by the orthorhombic distortion could be the crucial ingredient driving the transition from the metal and superconductor to the insulator [Takenobu00]. Earlier work showed the Mott transition in orbitally d-degenerate lattice models to take place at larger values of
U/W
for larger degeneracy, roughly proportionally to
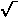 d
[Gunnarsson96][Koch99]. A strong enough ``crystal-field'' splitting of the threefold degenerate
t1u
molecular orbital of C60 caused by orthorhombic anisotropy could remove one or several bands away from the Fermi level, effectively reducing the orbital degeneracy d, thus shifting the Mott transition to a smaller critical value Uc/W. Exploring this concept, the basic question is how strong this splitting must be to promote such an effective reduction of degeneracy. In a non-interacting system, that reduction would clearly require a splitting magnitude similar to or larger than the full electron bandwidth W. In a strongly-interacting system, it is important to understand whether influencing the metal-insulator transition will again require anisotropic splittings as large as the bandwidth, or else if some smaller energy scale will emerge in its place.
d
[Gunnarsson96][Koch99]. A strong enough ``crystal-field'' splitting of the threefold degenerate
t1u
molecular orbital of C60 caused by orthorhombic anisotropy could remove one or several bands away from the Fermi level, effectively reducing the orbital degeneracy d, thus shifting the Mott transition to a smaller critical value Uc/W. Exploring this concept, the basic question is how strong this splitting must be to promote such an effective reduction of degeneracy. In a non-interacting system, that reduction would clearly require a splitting magnitude similar to or larger than the full electron bandwidth W. In a strongly-interacting system, it is important to understand whether influencing the metal-insulator transition will again require anisotropic splittings as large as the bandwidth, or else if some smaller energy scale will emerge in its place.
In this paper we exploit dynamical mean-field theory[Georges96] (DMFT) to answer this question, studying the effects of a band splitting on the Mott transition of an orbitally degenerate, strongly correlated metal. For that purpose we adopt the simplest idealization, namely a d=2 orbitally degenerate Hubbard model with bandwidth W and on-site repulsion U, and mimic the noncubic anisotropy by a diagonal splitting Δ between the two bands. In this model, we study the T=0 phase diagram in the (U,Δ) plane, and examine in particular how the Mott transition is influenced by the splitting. As the aim of the calculation is understanding a simple, and possibly fairly general physical mechanism, we do not attempt a realistic calculation of the kind that was accomplished recently for Ni and Fe [Lichtenstein01].
The main result found is that the effect is remarkably strong at large U, where the anisotropy-induced transition between the correlated multi-band metal and the Mott insulator takes place very readily, in fact for Δ << W. We interpret that as follows. The metallic band, originally of width W, is renormalized in the strongly correlated metal into a narrower ``Kondo-like'' quasiparticle peak of width zW, with 1>> z -> 0 as U-> Uc. Close enough to the isotropic and orbitally degenerate Mott transition at U\lesssim Uc, the correlated two-band metal can be driven effectively one band by a splitting as small as the Kondo energy scale Δ ~ zW. The one-band metal, in turn, has a lower Uc, so that the resulting state is an insulator.
With this model result in hand, we move on to consider NH3K3C60, where we carry out a DFT-LDA (density functional theory in the local density approximation) electronic-structure calculation to extract an order of magnitude for the effective orthorhombic splitting parameter Δ/W, found to be of order 0.25. Despite the obvious differences between the two-band Hubbard model and the true three band system, we suggest that the orthorhombic splitting will similarly drive the initially cubic fulleride with a small quasiparticle residue z from metal to insulator. In turn, in the light of our simple-model phase diagram, the return to metallicity of the ammoniated orthorhombic fulleride under pressure leads to an interesting question regarding the effective number of bands in that metal. It is finally concluded that anisotropy is likely a relevant element in promoting the Mott state in this material.
This paper is organized as follows: Section model:sec introduces the model and deals with its simple limiting cases. The calculation and results within the DMFT are described in Sec. dmft:sec. The t1u band structure of NH3K3C60 and its splitting due to anisotropy are described in Sec. bands:sec. The discussion and conclusions are finally presented in Sec. discussion:sec.
We work with the simplest two-band Hubbard model, assuming purely diagonal hoppings between orbitals on different sites, the anisotropic symmetry lowering all embodied in a diagonal on-site splitting term. We write the Hamiltonian as:
H = - t Σ< i,j>,σ Σα=1,2 (c+iασ cjασ + H.c. ) + Σi Σα=1,2 εα niα + U/2 Σi ni(ni-1) ,
where
c+iασ
creates a spin-σ electron in orbital
α
at site i, niα=Σσ c+iασ ciασ,
ni=Σα niα
is the total number of electrons at site i, and
< i,j >
denotes nearest-neighbor sites. The first term is a standard tight-binding hopping, simplified to ignore nondiagonal hopping, and also merohedral disorder, both of them present in the real systems. The second term introduces the anisotropic splitting
Δ
as a shift of the on-site orbital energy ε2=-ε1=Δ/2. The last term is the Hubbard on-site interaction, which we take in its simplest form, omitting for example any additional intrasite Hund's rule interaction terms. We also ignore the on-site electron-vibron couplings and the ensuing Jahn-Teller effects, even if quite important for other aspects[Gunnarsson97][Capone01][MTA].
In the U=0 limit, the splitting Δ>0 simply operates a rigid shift of band 2 upwards with respect to band 1, promoting electron transfer from the upper to the lower band. Above a critical value Δ=Δc and for a total electron filling n<2, the upper band is emptied up. For example, with two symmetric bands of width W and n =1 electrons per site, the upper band is emptied above Δc/W=0.5. At zero temperature (where we shall restrict ourselves in this paper) and zero interaction, U=0, the transition between the ``two-band metal'' and ``one-band metal'' is continuous. Because the topology of the Fermi surface changes, this transition is accompanied by a weak singularity of the total energy first described by Lifshitz[Lifshitz60]. When the electron-electron interaction U is turned on, one expects the emptying of the upper band to take place at smaller values of Δc, owing to the effective band narrowing. Perturbatively in U one can show that
where the value of the coefficient γ>0 depends on details of the bands. In addition, electron-electron interactions might modify the nature of the metal-metal transition singularity relative to the noninteracting case[Katsnelson00], a point which we will not further address here.
We restrict ourselves to a filling of one electron per site, n=1, discarding the trivial case
n=2
where the large-Δ state is a band insulator, as well as noninteger n, where insulators are not possible. The
Δ=0
and
Δ->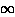 limits reduce then, respectively, to the (quarter-filled) two-band and (half-filled) single-band Hubbard models, both possessing a metal-insulator transition as a function of
U
[Rozenberg97][Rozenberg94][Caffarel94][Bulla99]. In particular, we are not interested in the weak-coupling antiferromagnetic instability of the ensuing large-Δ half-filled band, associated with nesting in specific hopping structures: we assume a genuine Mott transition for the half-filled single-band model to occur at a finite Uc
limits reduce then, respectively, to the (quarter-filled) two-band and (half-filled) single-band Hubbard models, both possessing a metal-insulator transition as a function of
U
[Rozenberg97][Rozenberg94][Caffarel94][Bulla99]. In particular, we are not interested in the weak-coupling antiferromagnetic instability of the ensuing large-Δ half-filled band, associated with nesting in specific hopping structures: we assume a genuine Mott transition for the half-filled single-band model to occur at a finite Uc1-band>0.
The limit of strong interaction, U>> W, is insulating for any value of Δ. This limit can be studied by mapping the model (hamiltonian:eq) onto a spin and orbital exchange Hamiltonian which reads[Arovas95]
Hexch = J Σ< i,j> ( Si· Sj + Ti· Tj + 4 Si· Sj \ Ti· Tj ) -Δ Σi Tzi ,
where the pseudospin-1/2 operators
Tj=1/2 Σαβν c+jαν σαβ cjβν
represent the orbital degrees of freedom, and J=2t2/U. For
Δ=0
this model has been studied both in one[Sutherland75] and two dimensions [Zhang98], with suggestions that interesting spin-liquid physics could be realized. For our purposes, it suffices to note that the model has no ferro-orbital instability, and has therefore a finite
q=0
orbital susceptibility. As a consequence it takes a nonzero value of
Δ
to fully orbitally polarize the ground state. Due to the absence of cross-band terms in the kinetic energy, complete orbital polarization occurs at a finite Δc~ J=2t2/U. For
Δ\ge Δc
that ground state is represented by a one band Mott insulator plus a totally empty split-off band.
Notice, finally, that for the specific case we are interested in (n=1 electron in a two-fold degenerate band) no orbital ordering is present at weak coupling. On the other hand, the possibility of antiferro-orbital and/or spin ordering within the Mott insulating phase, and of spin-orbital density waves in the intermediate U regime, depends crucially on the details of the hoppings and lattice coordination, which are left out of the infinite-dimensional lattice used in the calculations described in the following section. Therefore, within the standard scheme of single-site DMFT calculations, we study the phase diagram of this model restricted to spin and orbital paramagnetic states.
We have now all the elements to illustrate the general layout, sketched in Fig. phasedth:fig, of the zero-temperature phase diagram of model in Eq. (hamiltonian:eq) as a function of
(U,Δ)
for
n=1
electron per site. We stress the fact that we only consider the issue of the metal-insulator transition, restricting ourselves to paramagnetic states. This transition for n=1,
d=2
and Δ=0, previously studied in DMFT by the quantum Monte Carlo method [Rozenberg97], was found at
Uc2-band~ 1.5 W
at the relatively low temperature T=W/32. The same transition with
n=1
in the one-band model (d=1, or
d=2
at Δ=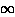 ) has been similarly calculated at
Uc
) has been similarly calculated at
Uc1-band ~ 1.3 W
also at T=W/32[Rozenberg94]. A finite temperature of course must affect somewhat these numerical values, but a common feature with our zero-temperature DMFT calculation described below, is that Uc2-band>Uc1-band. The AB line in Fig. phasedth:fig, representing
Uc
as a function of
Δ
and separating metals from Mott insulators, indicates this trend. The DM' line separates the fully orbitally polarized Mott insulator (at the right) from the two-band insulator, roughly as
Uc~Δ-1
for small Δ. Similarly, the CM line separates the fully orbitally polarized metal from the two-band metal: it starts from point C with a linear slope -γ-1, according to Eq. (smallU). In the region of full orbital polarization the value of
Δ
is irrelevant, and this is the reason why the Mott transition line MB is horizontal. As
Δ
increases, for
U<Uc1-band
the upper-band emptying transition takes the two-band metal across the CM line over to a one-band metal, while for
U>Uc1-band
it leads across the AM line to a Mott insulating state. The AM line starts off linearly at small Δ. Basically, this occurs since in close proximity of the Mott transition the relevant energy scale, to be matched by the orbital splitting Δ, is no longer the bare bandwidth, but rather the width of the Kondo-like quasiparticle peak of the correlated metal. That in turn is of the order of zW, which is smaller than
W
and proportional to the quasiparticle residue z, linearly vanishing with
(Uc2-band-U)
at the Mott transition[Georges96]. As the DMFT calculations will show, the effective emptying transition occurs when
Δ
increases to reach Δc(U)~ zW~ (Uc2-band-U).
The purpose of the DMFT calculations is to investigate this phase diagram in greater quantitative detail, in particular in the region of intermediate U~ W and Δ\lesssim W. We have implemented DMFT in the exact diagonalization flavor [Georges96][Caffarel94] for the degenerate Hubbard model on the Bethe lattice [DMFTdetails:note]. The advantage of the exact diagonalization method over the Monte Carlo approach in the solution of the impurity problem rests primarily in its being less computationally intensive -- useful when studying the phase diagram of a model as a function of more than one parameter -- and in its ability to address zero-temperature properties [Georges96][DMFTMCdetails:note]. To investigate possible spin/orbital antiferro correlations in NH3K3C60 [margadonna], one should study a detailed three-dimensional model, including the highly directional hopping matrix elements between different C60 sites (and possibly merohedral disorder). These bear no resemblance to the possible spin/orbital antiferro instabilities of the DMFT model, based on the idealization of the Bethe lattice. We ignore altogether these states, restricting the calculation to spin and orbital paramagnetic states. The results of the DMFT calculations are summarized in Fig. phasediagram:fig.
The values we obtain for
Uc1-band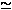 1.35 W
and Uc
1.35 W
and Uc2-band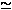 1.8 W, associated with the disappearance of the metallic state for one and two bands respectively, have been calculated with the same number of discretized bath levels per band nb=4. The associated error bar is estimated by repeating the calculation with nb=5. These values are in substantial agreement with corresponding values obtained by other methods[Rozenberg97][Rozenberg94][Caffarel94][Bulla99]. The other points in the phase diagram are obtained by following the stability of the two-band metal for a given value of
U
and increasing Δ, marking the emptying transition to the one-band metal or to the insulator.
1.8 W, associated with the disappearance of the metallic state for one and two bands respectively, have been calculated with the same number of discretized bath levels per band nb=4. The associated error bar is estimated by repeating the calculation with nb=5. These values are in substantial agreement with corresponding values obtained by other methods[Rozenberg97][Rozenberg94][Caffarel94][Bulla99]. The other points in the phase diagram are obtained by following the stability of the two-band metal for a given value of
U
and increasing Δ, marking the emptying transition to the one-band metal or to the insulator.
A deficiency of this single-site DMFT calculation -- which is restricted as usual to paramagnetic states only -- is the absence of a two-band insulating state for Δ>0. In fact, the suppression of the antiferro orbital fluctuations embodied in the exchange model (Hexch) produces a fictitious infinite uniform orbital susceptibility which leads to full orbital polarization as soon as
Δ
is turned on [Georges96]. Despite this limitation, the results of the present calculations are suggestive, revealing the announced sharp reduction of the metal-insulator
Uc(Δ)
for small but finite Δ. Indeed, our calculations give a
Δc(U)
which is roughly proportional to the quasiparticle residue
z(U)
of the undistorted (Δ=0) correlated metal at U<Uc2-band,
Δc(U)/W ~ β z(U) ,
with a proportionality constant β 0.3. Since
z(U)
vanishes as U-> Uc
0.3. Since
z(U)
vanishes as U-> Uc2-band, most likely linearly in
(Uc2-band-U)
[Georges96], even a very small
Δ/W
can be enough to cause a metal-insulator transition in the strongly correlated metal. For example, following the bold arrow at
U=1.5 W
in Fig. phasediagram:fig, a
Δ
value as small as
0.08 W
is sufficient to cross the transition line from the metal to insulator.
Further illustrating that, in Fig. specdens:fig we show the behavior of the spectral density
Aα(ω)=-π-1 Im Gα(ω) ,
Gα(ω)
being the one-particle Green's function of band α, on both sides of the metal-insulator transition. The asymmetry of the upper-band spectral density
A2(ω)
(solid lines) is very pronounced, as this band is nearly (Δ/W=0.07) or completely (Δ/W=0.08) empty. As soon as the Kondo-like peaks of the two bands differ enough in energy to induce the emptying of band 2, the lower-band spectral density
A1(ω)
takes the symmetric shape, characteristic of the half-filled one-band Hubbard model. Here the Kondo peak disappears completely, as this value of
U>Uc1-band
puts the Hubbard model of band 1 well inside the insulating regime. From the point of view of band 1, this transition can effectively be viewed as a doping-driven transition from a metal to a Mott insulator.
The above model calculations show that a small splitting Δ ~ zW of the orbitally degenerate band can drive the metal-insulator transition. We now wish to explore the implications that this result -- if assumed to be more general than the simple model where it was derived -- can have on the metal-insulator transition which takes place between isoelectronic K3C60 and NH3K3C60 (the former cubic and the latter orthorhombic) and on the insulator-metal transition of NH3K3C60 itself under pressure.
To obtain a quantitative estimate of the actual strength of anisotropy in the ammoniated fulleride, we carried out comparative DFT-LDA electronic-structure calculations for K3C60 and a simplified but meaningful model of NH3K3C60 using the PWSCF package based on plane waves and ultrasoft pseudopotentials[PWSCF:note]. We took a lattice constant a=14.2 Å for fcc K3C60, and a=14.89 Å for NH3K3C60, the latter with a centered tetragonal unit cell with c/a=0.91, neglecting the exceedingly small difference between a and b. In both calculations a single C60 unit cell was used, as pictured in Fig. geometryNH3:fig. In these model structures and calculations, we ignored merohedral disorder, as well as the rich antiferro-rotational structure recently discovered in actual NH3K3C60[margadonna].
We used 27 Ry and 160 Ry plane-wave energy cutoffs for the wave functions and the charge density, respectively. The Fermi surface was smeared with a parameter of 0.3 eV and a 2×2×2 Monkhorst and Pack mesh [Monkhorst74]. The density of states (DOS) was calculated as a sum of Gaussians of width σ=0.03 eV sampling k-space with a uniform 6×6×6 mesh.
Figure bandsNH3:fig shows the t1u bands of NH3K3C60 (a), compared to those of K3C60 (c); the corresponding densities of states are compared in panels (b) and (d). We find that the presence of the inserted NH3 molecules modifies only weakly the essentially pure C60 t1u conduction band, as expected. The difference in the two band structures is almost entirely due to the different lattice structures of the molecular centers. Small changes appear in the details of the bands throughout the Brillouin Zone, but both compounds are predicted in the LDA to be three-band metals, their overall t1u density of states not dissimilar in the ammonia-intercalated and pristine compound. In particular, as apparent from Fig. bandsNH3:fig(b), the bandwidths of NH3K3C60 and K3C60 are close, W~ 0.6 eV. The main difference in the two band structures is a splitting of the threefold-degenerate t1u band of K3C60 at the Γ point of NH3K3C60. This splitting is precisely a measure of the strength of the non-cubic crystalline environment seen by the t1u orbital on each fullerene molecule in the orthorhombic structure of NH3K3C60. Its magnitude is roughly a quarter (0.2 - 0.3) of the total bandwidth; this represents the main result of the DFT calculation. If this material were an uncorrelated metal, this splitting would have no major consequences, just a change of shape of the Fermi surface. The consequences can be much more important due to strong correlations, as discussed below.
The Γ-point
t1u
band splitting -- see Fig. bandsNH3:fig(a) -- can be taken as a crude estimate of the value of Δ ~ 0.15 eV in NH3K3C60, corresponding to a dimensionless ratio Δ/W ~ 0.25. This value is of course too small to determine a complete emptying of one of the bare, uncorrelated bands, and indeed all three bands of NH3K3C60 still cross the Fermi energy EF. However, correlations play an important role in fullerides, where the value of
U
is believed to lie between 1 and 1.6 eV [Gunnarsson97], thus substantially larger than the bandwidth W. As the nonammoniated fullerides A3C60 are still generally in the metallic and superconducting phases, it is not unreasonable to assume that their value of
U/W
[Antropov92][Martin93][Koch99L] is in all likelihood only marginally smaller than the
Uc3-band
for the Mott transition in the half-filled
d=3
band cubic system. Indirect evidence that ordinary, uncorrelated electronic bands do not exist, and that the electron spectral function at
EF
can more reasonably be assimilated to a narrow, dispersionless Kondo-like resonance was provided for K3C60 by recent photoemission data[Goldoni01].
The analysis of the metal-insulator transition in our simplified two-band model suggests a mechanism for an anisotropy-induced Mott transition in a correlated multi-band fermionic system. Clearly, many ingredients which we have left out of our calculation are expected to be quantitatively important for a realistic description of the t1u-doped fullerides. However, we suggest that the mechanism which we have described in Secs. model:sec and dmft:sec, whereby a small orthorhombic splitting of the bands is capable, alone, of turning a strongly correlated metal into a Mott insulator, could be a qualitatively important ingredient in the description of these systems. Specifically, we suggest that, in the appropriate (U,Δ) phase diagram (sketched in Fig. phasedNH3:fig), the ammoniation of K3C60 into orthorhombic NH3K3C60 could correspond to a displacement[Uammoniated:note] similar to that indicated by an arrow in Fig. phasediagram:fig. Inspection of Fig. phasediagram:fig shows that, if U is close enough to Uc, even a value of Δ substantially smaller than what we have estimated for NH3K3C60 could suffice to drive that metal insulator transition. Very recent conductivity measurements [Kitano02] on the class of compounds NH3K3-xRbxC60 suggest indeed the orthorhombic distortion as the main ingredient driving the Mott transition in these systems.
We should stress that our picture does not exclude a role, in the metal-insulator transition, for the accompanying ammoniation-driven expansion of the lattice. That role is experimentally proved by the pressure-driven insulator-metal transition, where NH3K3C60 is transformed into a metal and a superconductor, despite the permanence of the orthorhombic structure[Margadonna01]. However a new, interesting, question raised in Fig. phasedNH3:fig is what kind of metal does one recover in NH3K3C60 under pressure, whether a three-band metal like the cubic K3C60, or a new effective two-band metal. The former might in effect require a smaller deformation. It would be very interesting in this regard if the Fermi-surface topology of NH3K3C60 could be studied under pressure.
Another interesting -- even if perhaps not practically straightforward -- test of this overall picture could be obtained by applying uniaxial stress to cubic superconducting fullerides of the A3C60 family. Contrary to the standard tendency of hydrostatic pressure toward metallization and lower superconducting Tc, the orbital splitting associated with the appropriate uniaxial strain could drive some of these compounds perhaps first toward higher Tc, and eventually Mott insulating. A similar suggestion has been recently put forward, in the context of field-induced superconductivity [schon00][Batlogg00], by Koch [Koch02], although on rather different grounds. Also, recent calculations [Wehrli01][Wehrli02] of the size and effects of the charge-inducing electric field on the two-dimensional C60 layer, in the field-induced geometry, suggest that this field induces splittings of the molecular levels which might in turn affect the electron and hole bands in a qualitatitevely similar way to the one we propose here for the orthorhombic field in three-dimensional fullerides.
In summary, we have investigated the role of a symmetry-breaking orbital splitting on the transition to a Mott insulating state in an initially orbitally degenerate strongly correlated multiband metal. The calculations, carried out in a highly idealized d=2 model, have unveiled the Kondo quasiparticle energy scale as that which the noncubic splitting magnitude must reach in order to induce the Mott transition even at constant bandwidth and effective Coulomb repulsion. The likely relevance of this main qualitative finding to the fullerides K3C60 and NH3K3C60 has been highlighted.
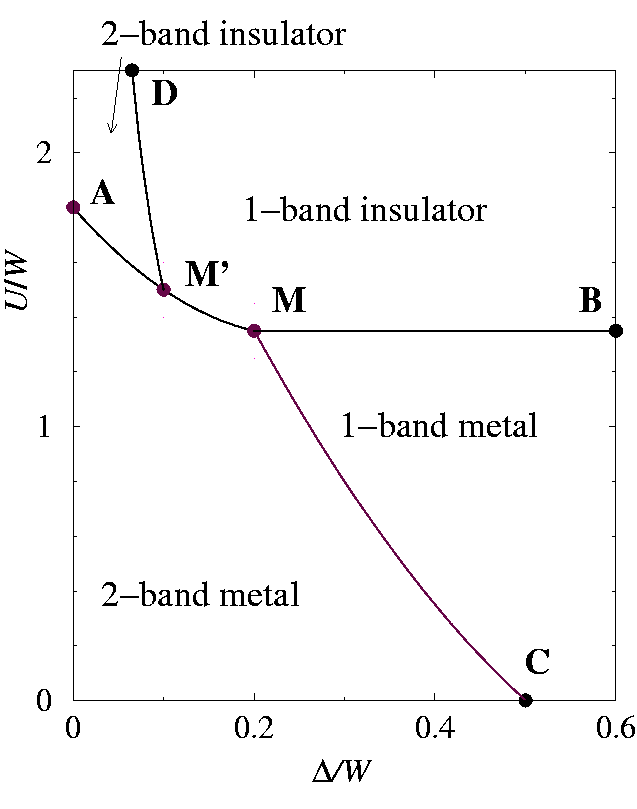
| Qualitative zero-temperature phase diagram for the two-band Hubbard model at quarter filling (one electron per site) in the U-Δ plane, where Δ is the anisotropy splitting of the two orbitals. The various phases and lines are described in Sect. dmft:sec. The multicritical points M and M' are not necessarily distinct. } |
Automatically converted from LaTeX by convert2html v. 3.21 [30 URL-ed refs]
| created: 20 Aug 2002 | last modified: 20 August 2002 by Nicola Manini |