Geometric Phases and Multiple Degeneracies in Harmonic Resonators
home | CM
Geometric Phases and Multiple Degeneracies in Harmonic Resonatorshome | CM |
 |
aInstitut Laue Langevin, B.P. 156, F-38042 Grenoble Cedex 9, France
bEuropean Synchrotron Radiation Facility, B.P. 220, F-38043 Grenoble Cedex, France
\today
PACS numbers: 03.65.Bz ]
Geometric phases may show up whenever the system under study depends on several parameters and is transported adiabatically around a closed path in parameters space[Berry]. Such phases have been predicted and observed in many different systems [Berry][Resta94][Delacretaz][Tycko87][Weinfurter90][Lauber94]. In particular, the cyclic phases observed by Lauber et al.[Lauber94] for a deformed microwave resonator have been recently accounted for within an approximate theory [manolopoulos]. However, the closed-path phases are not the only interesting observable quantities: for an open-path evolution, the phase of the projection of a parallel-transported [Anandan87] eigenstate on the initial eigenstate is equally well defined [Pancharatnam][Samuel88][Wagh98] whenever these two states are not orthogonal. The experiment of Ref. [Lauber94] measures also such phase relations for a number of intermediate points along the path. These phases can be compared with the theoretical outcome of the calculation of Ref. [manolopoulos]. We observe that the two sets of values disagree at half loop. The geometrical nature of these phases implies that the approximation of Ref. [manolopoulos] is missing the topological structure of the simple system at hand.
To find what is missing, we push the perturbative expansion of Ref. [manolopoulos] to higher order and demonstrate the presence of unsuspected extra degeneracies which account for the phase discrepancies. We show that similar ``satellite'' degeneracies close to a multiple degeneracy appear as a systematic, predictable feature of the Laplace operator in distorted domains: they can therefore arise in a broad range of undulatory phenomena, including acoustics, optics and quantum mechanics.
In Ref. [Lauber94] Lauber et al. follow the adiabatic evolution of three eigenstates of a microwave resonator driven along a loop in the two-dimensional space of deformations around the rectangular geometry. We indicate with
r = (r cos  , r
, r sin  )
the external parameter representing the displacement of the right upper corner of the cavity from the rectangular position (a,b)=(
)
the external parameter representing the displacement of the right upper corner of the cavity from the rectangular position (a,b)=( 3, 1)[sideb:note] at which the eigenstates |
3, 1)[sideb:note] at which the eigenstates | 1> = {2,4},
|
1> = {2,4},
| 2> = {5,3}
and
|
2> = {5,3}
and
| 3> = {7,1}
become degenerate [with
{nx,ny}
we indicate the wavefunctions
2
3> = {7,1}
become degenerate [with
{nx,ny}
we indicate the wavefunctions
2sin(nx x/a) sin(ny y/b)/ (a b)
in the rectangle]. We define the angle
(a b)
in the rectangle]. We define the angle
 so that it goes from
0
to
2
so that it goes from
0
to
2 following the path of distortions used in the experiment. In Fig. exp3waves:fig we report a sequence of adiabatic eigenfunctions
|
following the path of distortions used in the experiment. In Fig. exp3waves:fig we report a sequence of adiabatic eigenfunctions
| j(
j( )>
from the original pictures of Ref. [Lauber94].
)>
from the original pictures of Ref. [Lauber94].

|
The observed initial ( =0), intermediate ( =0), intermediate ( = = ) and final ( ) and final ( =2 =2 ) eigenstates of the microwave cavity deformed following adiabatically the path of Ref. [Lauber94]. } ) eigenstates of the microwave cavity deformed following adiabatically the path of Ref. [Lauber94]. }
|
The cyclic phase factors [ 1(2
1(2 )=-1,
)=-1,
 2(2
2(2 )=+1
and
)=+1
and  3(2
3(2 )=-1] are easily identified in Fig. exp3waves:fig from the recurrence of the pattern and the sign changes at
)=-1] are easily identified in Fig. exp3waves:fig from the recurrence of the pattern and the sign changes at
 =0
and 2
=0
and 2 . Similarly, the sign change of the central state
|
. Similarly, the sign change of the central state
| 2(
2( ) >
at
) >
at
 =
= tells us that its Berry-Pancharatnam open-path phase factor is
tells us that its Berry-Pancharatnam open-path phase factor is  2(
2( )=-1.
)=-1.
Let us compare now these results with those of the linear approximation[manolopoulos]. The eigenstates of the 2-dimensional Laplacian operator represent the normal modes of this cavity. The secular problem in the deformed domain can be conveniently reduced[manolopoulos] to the secular problem of the following differential operator
H(r)= 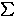 i,j
i,j  /
/ ui Mij(u,r)
ui Mij(u,r)  /
/ uj +D(u,r)
uj +D(u,r)
with vanishing boundary conditions in an undistorted rectangular domain for the transformed variables u. This form, given explicitly in Ref. [manolopoulos], is particularly suitable to set up a perturbation theory in r
H(r) = r H(1)( ) +r2 H(2)(
) +r2 H(2)( )+... ,
)+... ,
since all the parametric dependence is now in the functions
Mij(u,r)
and D(u,r). At first order it suffices to consider the subspace span by the three eigenstates of Lauber et al.'s experiment, and compute the
3× 3
matrices H(1)ij( )=<
)=<  i | H(1)(
i | H(1)( ) |
) |  j> . The form of this matrix, given in Ref. [manolopoulos], is
j> . The form of this matrix, given in Ref. [manolopoulos], is
where
F
and
F'
are real symmetric numerical matrices. In a sufficiently small neighborhood of the 3-fold degeneracy,
H(1)( )
accounts for the leading contribution to the energy shifts.
)
accounts for the leading contribution to the energy shifts.
|
The projection U22( )=< )=<  2(0)| 2(0)| 2( 2( )> calculated along the path of Lauber et al.'s experiment. Observation[Lauber94]: crosses (cf. Fig. exp3waves:fig). } )> calculated along the path of Lauber et al.'s experiment. Observation[Lauber94]: crosses (cf. Fig. exp3waves:fig). }
|
Manolopoulos and Child [manolopoulos] calculate the (real) transformation matrix U(1)ij( )= <
)= <  i(0)|
i(0)|  j(
j( )>, which diagonalizes
)>, which diagonalizes
H(1)( )
parallel-transporting the eigenstates. In particular,
U(1)ii(2
)
parallel-transporting the eigenstates. In particular,
U(1)ii(2 )
is the cyclic geometric phase of state i. Each calculated phase agrees with that observed experimentally. More generally, for any
)
is the cyclic geometric phase of state i. Each calculated phase agrees with that observed experimentally. More generally, for any  ,
U(1)ii(
,
U(1)ii( )/|U(1)ii(
)/|U(1)ii( )|
is the observable (open-path) Berry-Pancharatnam phase factor
)|
is the observable (open-path) Berry-Pancharatnam phase factor  i. These phase factors are therefore represented by the signs of the curves of Fig. 2b of Ref.[manolopoulos]. In Fig. thwavef:fig we report
U(1)22(
i. These phase factors are therefore represented by the signs of the curves of Fig. 2b of Ref.[manolopoulos]. In Fig. thwavef:fig we report
U(1)22( )
for the intermediate state |
)
for the intermediate state | 2> . Near
2> . Near  =
= , the disaccord with experiment is particularly evident: linear theory has U(1)22(
, the disaccord with experiment is particularly evident: linear theory has U(1)22( )
)  +1, while experimentally
+1, while experimentally  2(
2( )=-1.
)=-1.
\vbox{
| First order [manolopoulos] | Experiment [Lauber94] | 2nd order & BW | |
 2 2 | +1 | -1 | -1 |
 13 13 | -1 | +1 | +1 |
 2
and
2
and
 13
for the open path
13
for the open path
 1
going from
1
going from
 =0
to
=0
to
 =
= in the space of deformations. } \end{table} }
in the space of deformations. } \end{table} }
Around  =
= ,
|U11|
and
|U33|
are very small (<< 1): the interesting geometric phase information is contained in the off-diagonal part of the matrix
U(
,
|U11|
and
|U33|
are very small (<< 1): the interesting geometric phase information is contained in the off-diagonal part of the matrix
U( )
[ManPis]. In particular, in this case
)
[ManPis]. In particular, in this case
 13(
13( ) = U13(
) = U13( ) U31(
) U31( )/ |U13(
)/ |U13( ) U31(
) U31( )|
is the only observable phase associated to state 1 and 3, since |U13(
)|
is the only observable phase associated to state 1 and 3, since |U13( ) U31(
) U31( )|~ 1. From Fig. exp3waves:fig one can read U13(
)|~ 1. From Fig. exp3waves:fig one can read U13( ) ~ +1, and U31(
) ~ +1, and U31( ) ~ +1. Thus the observed
) ~ +1. Thus the observed  13=+1. We have verified that the linear theory of Ref. [manolopoulos] gives instead
13=+1. We have verified that the linear theory of Ref. [manolopoulos] gives instead  13=-1.
13=-1.
A similar reasoning can be applied to the path
 2
leading back from
2
leading back from
 =
= to
to  =2
=2  . The observed and calculated phase changes for this second path are the same as those for path
. The observed and calculated phase changes for this second path are the same as those for path
 1
going from
1
going from
 =0
to
=0
to  =
= : they are summarized in Table gammas:tab.
: they are summarized in Table gammas:tab.
The failure of the linear approximation in predicting the correct geometrical phase factors suggests that it misses the topological structure of degeneracies in parameters space. In this Letter, we investigate this issue by considering both the next order in the expansion (expansion:eq) and an exact numerical solution.
|
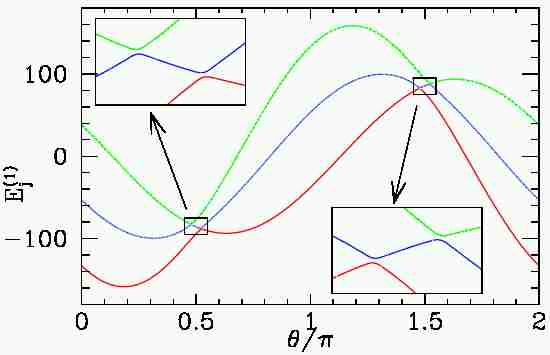
Linear correction E(1)j( ) [eigenvalues of H(1)( ) [eigenvalues of H(1)( )] to the energies of the three states considered in the text as a function of )] to the energies of the three states considered in the text as a function of  . } . }
|
The origin of the problem can be understood from inspection of Fig. energy:fig. Indeed, close to
 =
=  /2
and 3
/2
and 3 /2, the eigenenergies of
/2, the eigenenergies of
H(1)
get pairwise very near (the minimum splittings being
~ 1%
of those in the
 =0
direction). In this region, the linear approximation breaks down for
r
much smaller than in the (say)
=0
direction). In this region, the linear approximation breaks down for
r
much smaller than in the (say)
 =0
direction. Second-order terms can close the gaps inducing additional degeneracies in these directions, remaining dominant with respect to third- and higher-order ones. It is the smallness of the first-order splitting coefficient in this direction
=0
direction. Second-order terms can close the gaps inducing additional degeneracies in these directions, remaining dominant with respect to third- and higher-order ones. It is the smallness of the first-order splitting coefficient in this direction
 =
= /2
and
3
/2
and
3 /2
that makes this possible.
/2
that makes this possible.
We compute therefore the second-order Hamiltonian correction[Landau3]:
H(2)ij = <  i | H(2) |
i | H(2) | j> +
j> +  k
k 1,2,3 <
1,2,3 <  i | H(1) |
i | H(1) | k> <
k> <  k | H(1) |
k | H(1) | j>/Ei-Ek
j>/Ei-Ek
To calculate explicitly H(2), we cutoff the sum of Eq. (h2:eq) for |Ei-Ek| < Emax. Convergence is achieved including
~ 102
states. We have thus obtained the real symmetric numerical matrices G, G', and
G''
in H(2)( ) = G + G'
) = G + G' cos 2  + G''
+ G'' sin 2  . This second-order contribution adds to the linear Hamiltonian (Hfirstorder) to constitute the secular problem for the matrix
. This second-order contribution adds to the linear Hamiltonian (Hfirstorder) to constitute the secular problem for the matrix
We thus obtain the eigenvalues and eigenvectors of (Hsum:eq) as analytical functions of
r
and  . Like in the linear case, the transformation matrix
U(2)ij(r,
. Like in the linear case, the transformation matrix
U(2)ij(r, )
contains all the phase information of the eigenvectors. Now, at second order, all the geometrical phases, both for the closed loop and for the open-path, agree with experiment [Lauber94] (cf. Tab. gammas:tab and Fig. thwavef:fig).
)
contains all the phase information of the eigenvectors. Now, at second order, all the geometrical phases, both for the closed loop and for the open-path, agree with experiment [Lauber94] (cf. Tab. gammas:tab and Fig. thwavef:fig).
To elucidate the differences between first and second order, we show in Fig. exppath:fig the region of validity of the linear approximation. The endpoints W and Z of the open path
 1
considered above lie both well within this region. In addition, there exists a path
1
considered above lie both well within this region. In addition, there exists a path
 3
connecting W to Z, lying all inside the linear region on the same side of the 3-fold degeneracy. For path
3
connecting W to Z, lying all inside the linear region on the same side of the 3-fold degeneracy. For path
 3
the first-order theory is sufficient to predict the correct phases. Consider now the loop
3
the first-order theory is sufficient to predict the correct phases. Consider now the loop
 1 -
1 -  3
(
3
( 3 is followed backwards from Z to W). If no degeneracies were present inside, the cyclic phase factors
3 is followed backwards from Z to W). If no degeneracies were present inside, the cyclic phase factors
 2
2 1 -
1 -  3
would be
+1
for all states. Then the open-path phases
3
would be
+1
for all states. Then the open-path phases
 2
2 1
and
1
and
 2
2 3
would have to coincide. The same applies to the off-diagonal
3
would have to coincide. The same applies to the off-diagonal
 13
[ManPis]. Different phases in first and second order calculations indicate additional conical intersections of the second-order Hamiltonian (Hsum:eq) inside the loop.
13
[ManPis]. Different phases in first and second order calculations indicate additional conical intersections of the second-order Hamiltonian (Hsum:eq) inside the loop.
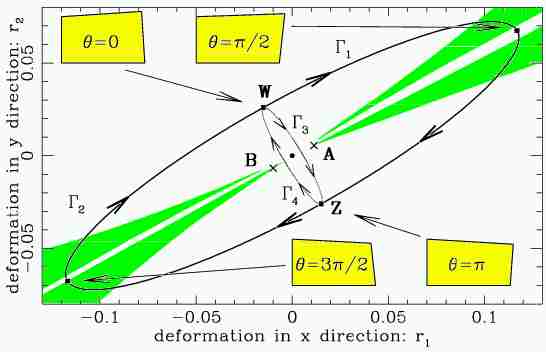
|
The path  1+ 1+ 2 in r space used in experiment [Lauber94]. The 3-fold degeneracy sits at the origin. The four deformed rectangles represent the shape of the resonator at four representative points along the path. The two crosses mark the positions of the satellite 2-fold degeneracies A and B. The non-shaded region is where the linear approximation for the gaps is correct within 50%. } 2 in r space used in experiment [Lauber94]. The 3-fold degeneracy sits at the origin. The four deformed rectangles represent the shape of the resonator at four representative points along the path. The two crosses mark the positions of the satellite 2-fold degeneracies A and B. The non-shaded region is where the linear approximation for the gaps is correct within 50%. }
|
Indeed, we find that, at the points A (rA 0.0126,
0.0126,  A
A 1.64) and B (rB
1.64) and B (rB 0.0120,
0.0120,  B
B 4.64) of Fig. exppath:fig, the two lowest eigenvalues are degenerate. Knowledge of the phases in the linear region around the threefold degeneracy at the origin [manolopoulos] together with the presence of the twofold conical intersections at A and B accounts for all (open-path and cyclic) phases. In particular, on the complete loop
4.64) of Fig. exppath:fig, the two lowest eigenvalues are degenerate. Knowledge of the phases in the linear region around the threefold degeneracy at the origin [manolopoulos] together with the presence of the twofold conical intersections at A and B accounts for all (open-path and cyclic) phases. In particular, on the complete loop  1 +
1 + 2, the two sign changes that
|
2, the two sign changes that
| 1>
and
|
1>
and
| 2>
acquire encircling A and B cancel out: as a fortuitous coincidence, the observed cyclic Berry phases end up being the same as these obtained in the linear theory[manolopoulos].
2>
acquire encircling A and B cancel out: as a fortuitous coincidence, the observed cyclic Berry phases end up being the same as these obtained in the linear theory[manolopoulos].
As well known[VonNeumann] for a generic real Hamiltonian it is necessary to vary two parameters in order to make a degeneracy occur accidentally, i.e. not on account of symmetry. In other terms, the codimension of the degeneracies is two. Thus, in our two-parameter system, 2-fold degeneracies occur at isolated points. Therefore, a small readjustment of the two parameters can always compensate a sufficiently small perturbation to the Hamiltonian: the conical intersections will only displace slightly upon inclusion of third- and higher-order corrections of expansion (expansion:eq). The fact that the expansion parameter r at the degeneracies is so small indicates that, most likely, higher-order corrections are indeed smaller that the r2 term at the degenerate points and even beyond them. In this case, higher-order terms do not change the qualitative configuration of degenerate points and do not affect therefore the geometrical phases calculated at second order. However, without an upper bound on the higher-order terms, nothing guarantees that these terms do not displace significantly or even remove the degenerate points found at second order.
For this reason, we need to verify with a nonperturbative method the actual presence and position of the degeneracies. We thus resort to the numerical technique introduced by Berry and Wilkinson[BerryW] (BW) to solve the Laplace problem in two-dimensional domains. The advantage of this method is to reduce the two-dimensional differential equation to a one-dimensional integral equation for the normal derivative of the wavefunction at the boundary, which can be solved on a discrete mesh. We assess the presence of each degeneracy by encircling it with a loop in the parameters space and calculating the cyclic Berry phases of the involved states with the BW numerical method. Specifically, for the problem at hand we have calculated with the BW technique[NumberN:note] the Berry phases for the (discretized) loop
 1 -
1 -  3
in Fig. exppath:fig, obtaining
3
in Fig. exppath:fig, obtaining  1=-1,
1=-1,  2= -1, and
2= -1, and  3=+1. Similar procedure also confirms the presence of the degenerate point B.
3=+1. Similar procedure also confirms the presence of the degenerate point B.
At this stage, one may wonder if satellite degeneracies (i.e. degeneracies within the range of validity of perturbation theory, involving irrelevant components on states outside the multiplet) are present only in this specific distorted ``quantum billiard'', or if they are a widespread feature. Consider, for example, the 3-fold degenerate multiplet {nx,ny}={1,3}, {4,2}, and
{5,1}
in the same geometry a/b= 3: in this case we find no satellite degeneracies in the neighborhood of the 3-fold one, where second-order perturbation theory holds. This is not surprising, since over the whole range 0<
3: in this case we find no satellite degeneracies in the neighborhood of the 3-fold one, where second-order perturbation theory holds. This is not surprising, since over the whole range 0< <2
<2 , the first-order splittings vary much more slowly than those of Fig. energy:fig. Thus, when the quadratic term becomes of the same order of the linear term, also higher-order terms are of comparable size.
, the first-order splittings vary much more slowly than those of Fig. energy:fig. Thus, when the quadratic term becomes of the same order of the linear term, also higher-order terms are of comparable size.
If we could establish a general criterion to predict the occurrence of satellite degeneracies for the general case of a n-fold degenerate multiplet in a billiard of arbitrary side ratio a/b[sideb:note], then we could easily realize practical classical/quantum systems with clustered conical degeneracies, and thus intricate patterns of parallel-transported wavefunctions. Satellite degeneracies are to be expected whenever (i) the smallest first-order gap
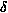 (1)
(1) /2
near
/2
near
 =\/pi 2
is much smaller than those
=\/pi 2
is much smaller than those
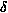 (1)0
at
(1)0
at  =0, and (ii) the second-order matrix elements of |
=0, and (ii) the second-order matrix elements of |H(2)( /2)|>>
/2)|>> 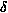 (1)
(1) /2, so that for
r~
/2, so that for
r~ 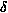 (1)
(1) /2/|
/2/|H(2)ij( /2)|<< 1
first and second order terms are of the same magnitude and at the same time higher-orders are negligible
/2)|<< 1
first and second order terms are of the same magnitude and at the same time higher-orders are negligible
We first look for the realization of condition (i).
H(1)( )
[Eq. (Hfirstorder)] determines the first-order splittings
)
[Eq. (Hfirstorder)] determines the first-order splittings 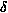 (1)
(1) . The diagonal matrix elements of
F
determine the linear splittings
. The diagonal matrix elements of
F
determine the linear splittings
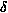 (1)0
since the off-diagonal elements either vanish or are much smaller. The diagonal matrix elements of
F'
are instead all equal. Consequently, at
(1)0
since the off-diagonal elements either vanish or are much smaller. The diagonal matrix elements of
F'
are instead all equal. Consequently, at  =
= /2, the mixing and the splittings
/2, the mixing and the splittings
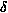 (1)
(1) /2
of the three states are governed by the off-diagonal elements of F'. A parity selection rule applies to these matrix elements:
F'{nx,ny}{n'x, n'y}
is zero when
/2
of the three states are governed by the off-diagonal elements of F'. A parity selection rule applies to these matrix elements:
F'{nx,ny}{n'x, n'y}
is zero when
In addition, the the nonzero elements (setting a=b for the sake of an estimate) satisfy
|F'{nx,ny}{n'x, n'y}|  29/2 nx/n'x n'y/ny /{ [1-(nx/n'x)2] [1-(n'y/ny)2] } .
29/2 nx/n'x n'y/ny /{ [1-(nx/n'x)2] [1-(n'y/ny)2] } .
For states widely separated in
nx - ny
plane (nx/ n'x << 1 and n'y / ny<< 1) this coupling becomes very small. Small linear gaps occur at
 /2
whenever a state
{nx,ny}
in the degenerate multiplet is weakly coupled to the others, i.e. when all the off-diagonal matrix elements
F'{nx,ny}{n'x n'y}
are much smaller than
/2
whenever a state
{nx,ny}
in the degenerate multiplet is weakly coupled to the others, i.e. when all the off-diagonal matrix elements
F'{nx,ny}{n'x n'y}
are much smaller than 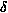 (1)0. Indeed in Lauber's multiplet the linear coupling between states
{5,3}
and
{7,1}
vanishes because of parity (parity:eq), and the coupling determining
(1)0. Indeed in Lauber's multiplet the linear coupling between states
{5,3}
and
{7,1}
vanishes because of parity (parity:eq), and the coupling determining
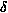 (1)
(1) /2
is F'{2,4}{7,1}~ 0.9, compared to
/2
is F'{2,4}{7,1}~ 0.9, compared to 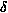 (1)0~ 50. As we saw, for the multiplet {1,3}, {4,2}, and
{5,1}
the ratio
(1)0~ 50. As we saw, for the multiplet {1,3}, {4,2}, and
{5,1}
the ratio
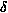 (1)
(1) /2/
/2/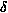 (1)0
is much closer to one, and indeed, no satellite degeneracies appear there.
(1)0
is much closer to one, and indeed, no satellite degeneracies appear there.
We come now to condition (ii). The matrix elements of
H(2)( /2)
follow no selection rule. We have verified that these matrix elements are large: for instance |
/2)
follow no selection rule. We have verified that these matrix elements are large: for instance |H(2){n,n+1}{n+1,n}( /2)|~ n3. These matrix elements reduce rapidly as a function of the distance
(nx-n'x)2+(ny-n'y)2
between the states.
/2)|~ n3. These matrix elements reduce rapidly as a function of the distance
(nx-n'x)2+(ny-n'y)2
between the states.
In conclusion, whenever in a degenerate multiplet one state is near some states (so that second-order coupling is large) for which selection rule (parity:eq) makes first order coupling vanish, and at the same time it is far from all remaining states (so that
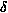 (1)
is small), one expects satellite degeneracies. This rule permits, for instance, to decide that the 3-fold multiplet {1,5}, {4,4},
{6,2}
for
a/b=
(1)
is small), one expects satellite degeneracies. This rule permits, for instance, to decide that the 3-fold multiplet {1,5}, {4,4},
{6,2}
for
a/b= (5/3)
has a structure of satellite degeneracies very similar to that of Lauber's experiment, as we then verified by BW calculation.
(5/3)
has a structure of satellite degeneracies very similar to that of Lauber's experiment, as we then verified by BW calculation.
An interesting case emerges from this analysis: when all off-diagonal matrix elements of
F'
vanish because of selection rule (parity:eq), the linear perturbation does not remove the degeneracy at  =
= /2. In this direction, the second-order term
/2. In this direction, the second-order term
H(2)
is therefore the leading responsible for the splitting of the degenerate levels, which therefore ``kiss'' gently, instead of intersecting conically as usual. Many two-fold degenerate multiplets satisfy this condition (for example
{2,4}
and
{4,2}
for a/b=1, or
{2, 3}
and
{6, 1}
for a/b=2).
In this work, we have accounted for all experimental findings regarding the eigenstates of Lauber et al.'s deformed resonator. We have found that in deformed rectangular resonators additional degeneracies (with lower multiplicity) may appear very close to multiple degeneracies. These extra degeneracies are responsible for the observed pattern of geometric phases. These results rely only on the properties of the Laplace operator: for this reason they have a wide scope of applicability and are not restricted to simple microwave resonators.
We thank Dirk Dubbers for suggesting us to investigate this system and for useful discussions.
Automatically converted from latex by convert2html v. 2.93
| created: 17 April 2000 | last modified: 8 January 2026 by Nicola Manini |