The quantum mechanical basis of harmonic vibrational states involved is naturally organized in "tiers": the first tier includes only states directly coupled to the bright state by anharmonic terms. The second tier lists states coupled to those of tier 1, and so on. The basic idea of the tier by tier basis generation is illustrated in the following animation for a 2-oscillator model system:
Our method of choice to compute the spectrum, the "tiers model" was initially proposed in a simplified version by A. A. Stuchebrukhov and R. A. Marcus, J. Chem. Phys. 98, 6044 (1993). It takes advantage of the hierarchical structure of the basis to calculate the spectral function (imaginary part of a Green function matrix element), by recursive matrix inversions within each tiers subspace, instead of the whole Hilbert space.
To keep the size of the matrix to invert under control, the growth of the number of states with successive tiers is cut off at some arbitrary maximum number of states (40, in the calculation of the picture): this originates the irregular patterns, the asymmetric shape of the tiers, and the final detachment from the v2 axis. The choice of "kept" states is basically based on the "perturbing strength", the ratio of the matrix element to the difference in energy with the generating state: |Vij/(Ei-Ej)|.
Without this truncation, the Green function method is asymptotically exact, as we have verified by letting the number of tiers become fairly large, and computing the excitation spectrum of a single oscillator, where comparison with exact solutions of the Schrödinger on a discrete mesh are easily available.
According to our tests, the method is converging fairly well as the number of states per tier and the number of tiers are let grow. This method is extremely easy to run in parallel.
The main difficulty in applying this method (or any other nonperturbative method, e.g. a Lanczos diagonalization) to real molecules is intrinsic to the polynomial expansion of the potential. Calculations only converge below an energy border, basically given by the lowest saddle point of the polynomial potential, above which the wave function leaks out to the non-lower-bound potential region. In practice, the height of this saddle-point is similar for many polyatomic molecules, in the range 1000-10000 cm-1, as it is determined by the degree of anharmonicity of the chemical bonds, which is fairly universal. (It is actually getting generally lower as the number of vibrational degrees of freedom increases, as more "dissociative" paths open in new directions of configuration space.)
In practice, this limitation makes the exact Green function technique inapplicable to the energy range interesting for IVR.
The introduction of anharmonicity from the very beginning (e.g. basing the potential expansion on Morse potential) is therefore a necessary requirement for a rigorous and converging theory.
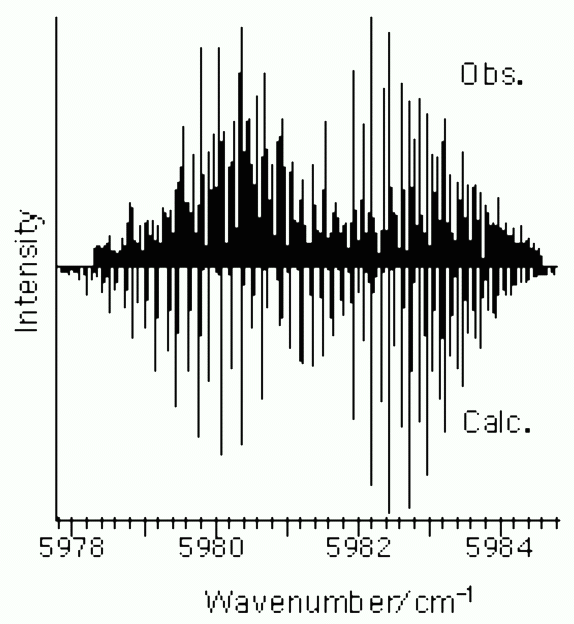
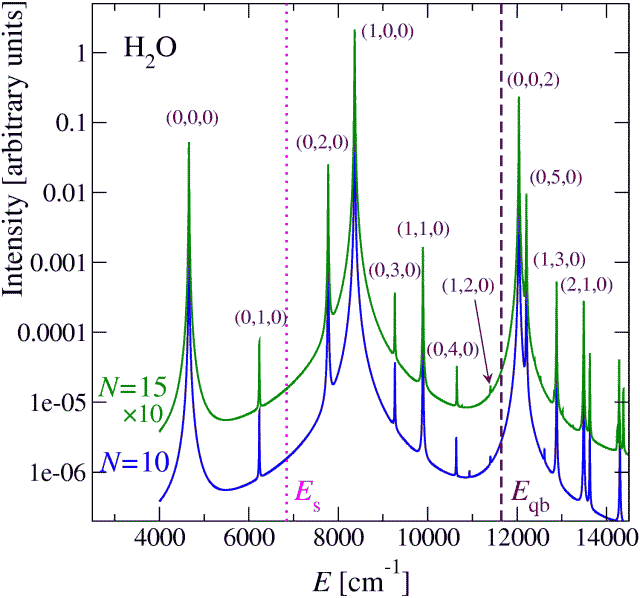
Here follows a sample spectrum of the water molecule (the bright state (1,0,0) has 1 quantum of the symmetric OH stretching mode), for which ab-initio frequencies and anharmonic coupling are available in the literature [A.G.Csaszar and I.M.Mills, Spectrochim. Acta A 53, 1101 (1997)]:
The latest version of the c++ code to compute molecular spectra (as that of
H2O above) based on the Green-function tier model,
is freely downloadable (zip
200 kB): it includes documentation plus
a few examples of input and output.
If you make good use of it, please cite:
A. Del Monte, N. Manini, L.G. Molinari, and G.P. Brivio,
Mol. Phys. 103, 689 (2005).