The ground state symmetry of the H ⊗ h model

Dynamic Jahn-Teller

A degenerate electronic state interacting with one (or several) vibrational modes, also degenerate.

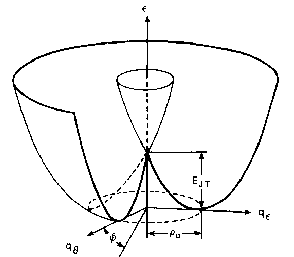
Traditionally: the ground state remains for any (linear) coupling of the same symmetry. How boring!

But why?
Because of a Berry phase!
In short, a degenerate vibronic state would not match the antiperiodic boundary conditions imposed by the change in sign of the electronic variables to the vibrational ones. So, the ground state has to be degenerate, and it turns out that the same degeneracy of the original electronic state prior to coupling is OK for all couplings.

For a review of the relation between Berry phase and ground-state symmetry, you may take a look to the following publications: J. Phys.: Condens. Matter 10, 8485 (1998) (preprint), Fullerenes. Recent Advances ... - vol. 5, ed. by K.M. Kadish and R.S. Ruoff (The Electrochemical Society, Pennington, NJ, 1997), pag. 468, Phys. Rev. B 49, 12998 (1994), and Manini's PhD thesis.

What about the H × h model?

Due to a special property of the symmetry group, the non-simple-reducibility, the form of the coupling is not completely dictated by symmetry. A new parameter,

, intervenes. For some values of this parameter, the Berry phase is not active on the low-energy paths of the coupled electron-vibration dynamics.

So what? Is the ground state changing symmetry?

Yes indeed. At large enough coupling g, the ground state changes symmetry when the new parameter α takes values in a rather wide interval surrounding the right angle. It becomes of A symmetry, that is nondegenerate, in the colored hilly region at the right, while remaining the usual H state in the blue flatlands. Specifically, in the figure at the right, we plot the gap (obtained numerically) between the lowest H and A states, only where it is positive, i.e. where the A state is lower.

Is this funny model relevant for any actually existing system?

Yes again. Of course, the symmetry needs to be that of the icosahedron. So, sorry folks, but no solid state! But nowadays there are several molecular icosahedral systems such as C₆₀ and some Si clusters. The ion C₆₀⁺ is a good example of an H electronic state, interacting with (several) h (and also g) modes. In principle, if the actual couplings in these systems do imply this symmetry change, then it should show up rather spectacularly in spectroscopy. Those interested may read the preprint or the published article. The real fans may check out early results [also, a competing group came up with related work a couple of months later].

created: 20 July 1999

last modified: 25 Feb 2019

by Nicola Manini