Any ''vector'' object which is parallel-trasported along a path back to the original place, may acquire an angle with respect to its initial direction prior to transport. This angle is a geometric property. Here, I illustrate (at a fairly elementary level) the basics and a few selected consequences of this almost ubiquitous phenomenon.
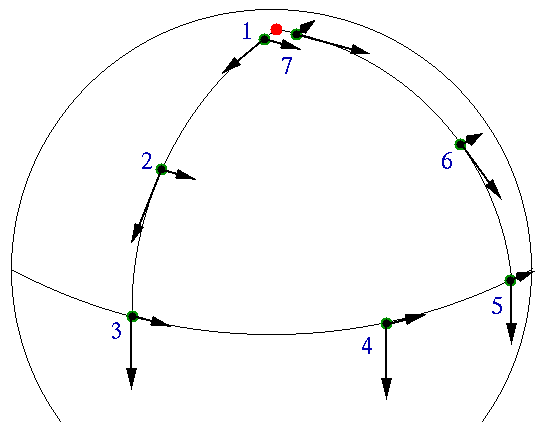
The reason for this rotation is purely geometrical-topological. In fact, it is connected to the intrinsic curvature of the sphere. No such phenomenon would appear if vectors are parallel-transported along a flat manifold, such as a plane or a cylinder. The rotation angle is in fact related to the integral of the curvature on the surface bounded by the loop.
Such rotation angles of geometrical origin are known as Berry phases. "Phase" is used meaning just "angle" for whatever possible argument of sin(·) or cos(·) or exp(i ·). Several specific cases had been recognized for many years, in particular the well-studied Aharonov-Bohm effect and Pancharatnam's work on the geometric phases in optics. M. Berry published in 1984 a very influential formal systematization of the closed-path geometric phase in quantum mechanical problems, some of which is summarized in the following paragraphs.
Indeed, Berry phases do not appear only in everyday experience of geometrical vectors. The ingredients of a parameterized vector field are present also in undulatory phenomena. A basic concept in math is that of sets of functions structured as vector spaces. Such functions often describe wave phenomena, such as the vibrations of a drum membrane. Each wave has a phase connected to its time evolution (the going up and down of each point of the membrane). This dynamical phase is not geometrical: it depends on the speed at which the parameterized path is followed, and on the arbitrary choice of a "zero phase" (technically called a gauge choice) at each point along the path. A recipe is needed to get rid of any dynamical phases, and single out the intrinsic, geometrical invariant phases. Berry' s work [M.V. Berry, Proc. R. Soc. Lond. A 392, 45 (1984)], contains a precise formulation of this concept, that is a realization of parallel transport for generic complex vectors.
States in quantum mechanics are represented by vectors in a linear (complex) space. In many cases they can be visualized as wave functions. There is no reason that they should make exceptions to the general rule of acquiring phase angles after parallel transport along loops.
A standard, though slightly simplified, formulation goes as follows: consider the set of eigenstates of a (self-adjoint) Hamiltonian operator H, depending on several classical ''external'' parameters (which again we indicate collectively as q). Changing q from one point to another in its multi-dimensional space, the set of stationary states and the related eigenenergies of H change in a completely generic way, leading to totally new and unrelated eigensystem. Assuming however smooth dependence of H on the external parameters q, one expects that for infinitesimal change in the parameters, also the states change by small amounts. The notion of parallel transport may be implemented by imposing that the inner product between a given eigenstate at some point q, and the evolved eigenstate at a following neighboring point q+Δq, be as close to 1 as possible (leading changes of order Δq2).
Note that each stationary state "rotates" (in the complex sense) as exp(-i Ek t/ ℏ) [where Ek is the energy of the state, t is time and ℏ is Planck's constant], because of its Schroedinger time evolution. On top of this, since at each point the eigensystem is unrelated to that at a different point, nothing forbids to multiply each eigenstate by an additional arbitrary phase factor exp[-iΦk(q)] (a "gauge choice")! The correct rule for the "parallel transport", as sketched above, permits to calculate the geometrical phase, such that it ignores completely any dynamical and gauge phase. The result depends only on the geometry of the loop. In this sense, Berry's phase is said to be "gauge-invariant".
Two classic examples of Berry phase in quantum mechanics (known long before Berry's systematization) are:
As you must have guessed, however, in most cases the Berry phase vanishes. As one might expect, usually coming back after a loop to the starting point, makes nothing important, and the vector quantities go back to exactly what they used to be before the loop, indicating that the space where those vectors are moved around is flat. So, nonzero phases are clues pointing to nontrivial topological properties underlying the relation between the vector quantities and the adiabatic parameters q.
In physical applications, one often encounters Hamiltonian operators depending on several external parameters, thus potentially affected by Berry phases. Two general kinds of such q-dependences can be distinguished:
A physically relevant and rather simple case is that of the eigensystem of a real Hamiltonian operator H depending on a set of external parameters q. The eigenstates of a real operator may always be chosen to be real, at any q-point. It is straightforward to check that continuous real eigenstates realize parallel transport. In the real case, is is therefore easy to get rid of complex phases such as exp(-i Ek t/ ℏ), coming from the time evolution.
This granted, it's clear that Berry's recipe for the phase at the end of any loop can only yield 0 or π, since any (nondegenerate) wave function must come back either to itself or to minus itself.
As usual, in 99% of the cases, the Berry phase turns out to be zero. However, it was clear right at the beginning that when some point of degeneracy is enclosed in the loop, the phase can be nonzero. By "point of degeneracy" we mean a q-point where the energy of the state under consideration becomes exactly the same as that of the state immediately above or below it. By "enclosed" we mean that the loop cannot be smoothly deformed to avoid surrounding the degenerate point.
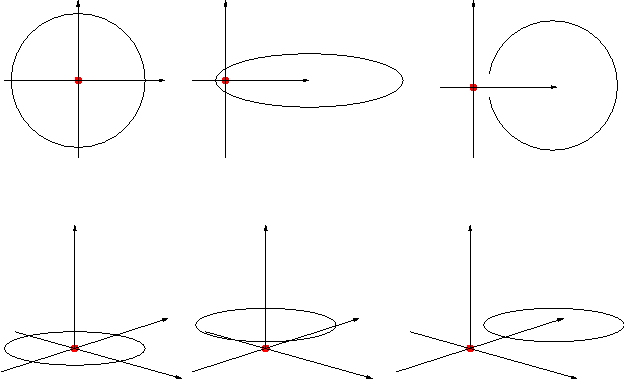
Nontrivial Berry phases of π can therefore appear only when the q-space with the degenerate q-points removed is multiply connected (an exquisitely geometric-topologic concept).
In conclusion, in the case of real Hamiltonians, the Berry phase along some path equals the number of level degenerate points that this path encloses times π.
Needles to say, in the Born-Oppenheimer separation of electronic and vibrational motion, the Berry phase is usually zero on any physically relevant path, since the electronic ground state is usually well separated from the first electronic excitation. The notable exception is the so-called Jahn-Teller (JT) effect. Here, the ground state is degenerate at some specially symmetric q-point. A distortion of the molecule/crystal reducing the symmetry corresponds to a displacement in q-space from that special point. This deformation can be energetically convenient: in this way the molecule/crystal undergoes a so-called JT distortion.
To fix the ideas, we consider here in some detail the instructive example of the triangular molecule (E × e JT model). The equilibrium geometry of a triangular cluster such as Xi3 is not the equilateral triangle, but a distorted isosceles geometry. Indeed in the equilateral configuration, the electronic ground state is twofold degenerate (E). These 2 electronic states split for any displacement away from the equilateral geometry. Due to symmetry, it is clear that equivalent isosceles distortions where any two Li atoms get closer are energetically equivalent.
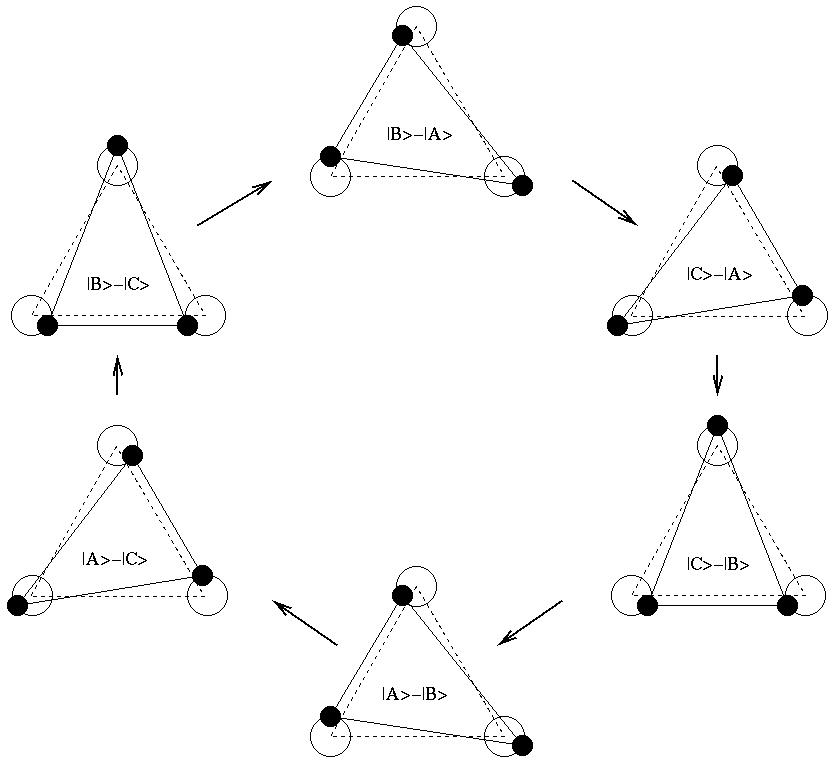
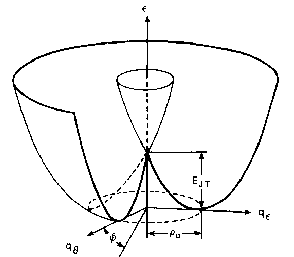
Actually, it may be verified that (for linear coupling) the equilibrium configurations constitute a flat circular valley - or trough - when the Born-Oppenheimer potential energy is plotted against the q coordinates. Note the degeneracy of the two Born-Oppenheimer potential energy sheets at the central q=0 high-symmetry point in the figure. So, this "JT valley" encircles a degeneracy point for the electronic (real) Hamiltonian: a Berry phase should therefore be present and, moreover, physically relevant, since this loop is frequently accessed by the low-energy dynamics of the q-distortions.
We can convince ourselves that the electronic wave function indeed undergoes a Berry phase change of π while the distortions loop around the trough, by a little meditation on the changes in the electronic wave function during a loop in the distortions space illustrated in the figure above. The real adiabatic choice of the electronic state is indicated, in terms of the three atomic s orbitals of the three Li atoms. Notice that we choose carefully the phase at each point in order to simulate "parallel transport", i.e. to have positive overlap to the immediately preceding configuration. A 2π loop along the JT valley is completed going from one configuration to that pictured at the opposite side: the electronic state changes sign. Another 2π loop is needed to restore the original sign.
In this representation of the electrons, the "pseudorotational" motion of the q-distortion, is just a free particle on a circle. Until the q-coordinates are treated as classical variables, no special effects are to be expected of the sign change in the electronic wave function, since geometric phase changes could be observed only by quantum interference. Even if the distortion might happen to follow the low-energy loop, the dynamics of the classical nuclei could not care less of the Berry phase acquired by the electrons. However, as soon as we recall the quantum nature of the q degrees of freedom (quantization of the phonons), their wave function gives a coherent amplitude of probability of being anywhere along the JT valley. This introduces interference of the electronic state before and after a nontrivial loop: for this reason the Berry phase acts as a boundary condition for the quantization along the JT valley.
In our example for the triangular molecule, the minus sign acquired by the electronic wave function after one loop needs to be compensated by another minus sign of the vibrational counterpart, since the overall (vibronic) molecular state needs to be represented by genuine single-valued wave function. The low-energy pseudo-rotational motion (described by a free-particle wave function of type exp(-i k Φ), where Φ is the angle parameterizing the trough) along the JT valley is dramatically affected by this Berry-phase-induced anti-periodic boundary condition: the quantization rule selects half odd integer pseudorotational "momenta" k, rejecting ordinary integer ones. Substantial consequences follow for the vibronic spectral properties, both in energetics (the JT energy gain is reduced, due to the larger amplitude of ''zero-point'' motion of the lowest k=±½ rotor state, instead of k=0 as would be without Berry phase), and in symmetry (the ground state would be singly degenerate without a Berry phase).
The role of the geometrical phase in determining the symmetry of the vibronic ground state is not restricted to the E × e model presented here, being instead very general in this kind of coupled electron-distortion systems.
A general consideration is due, at the end of this section. We must never forget the two logical steps we took introducing the Berry phase concept in JT systems. First, with the BO adiabatic approximation, we introduce a separation between ''fast'' and ''slow'' degrees of freedom, and a corresponding factorization of the vibronic wave function. Then, we treat the vibron degrees of freedom as classical variables, since the Berry phase needs a classical context for its description.
These two conceptual steps are actually approximations (the classical description of the vibrons is quickly released, as soon as the phases on the loops have been computed). They could in principle be avoided from the beginning, by diagonalizing the full e-v quantum Hamiltonian. In this sense, the Berry phase is an unnecessary semiclassical concept. However, as long as a Born-Oppenheimer factorization is considered useful, the Berry-phase concept is also a very useful framework for understanding, classifying and computing spectral properties of DJT systems. There are relevant examples of JT systems showing changes in ground state symmetry, that would be unexplained if the Berry-phase analysis were ignored.
Many generalizations have been proposed to the original definition. In particular, it was soon realized that there is no reason for the evolution to be adiabatic, i.e. slow: the phases turn out the same even if the external parameters move fast.
Also, why restricting to a loop at all? Indeed it is possible to define and measure Berry phases also for arbitrary open paths, provided that the evolved state at the end of the path is not orthogonal to the initial one.
Furthermore, does the path really need to be continuous? People like to compute quantities numerically, so there must be some discrete version of Berry's integral. Indeed there is a very natural one (in terms of Bargmann invariants), and it turns out so simple and pretty that it may be conveniently taken as an alternative fundamental definition of Berry's phase.
Also, why considering one single state? n degenerate states may evolve together, acquiring not just a phase factor [an element of the group U(1)], but a whole matrix [an element of the group U(n)]: this leads to the non-abelian phases of F. Wilczek and A. Zee, Phys. Rev. Lett. 52, 2111 (1984).
Finally, in-house research in Grenoble/Trieste/Milano lead us to one extra exciting generalization: off-diagonal geometrical phases.
Some of these generalization come out naturally if one considers the vectors as objects evolving in the ray space... but this is a rather complicate story: I suggest reading the cited articles by Aharonov, Simon, and Resta.
Taking a look to the following references may provide further insight in the fascinating concept of Berry's geometrical phase and its applications, with focus on ground-state symmetry in dynamical JT.