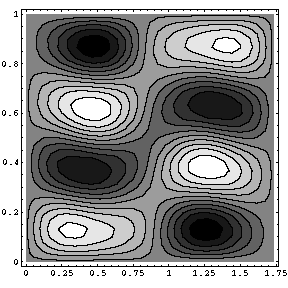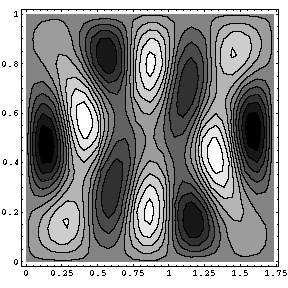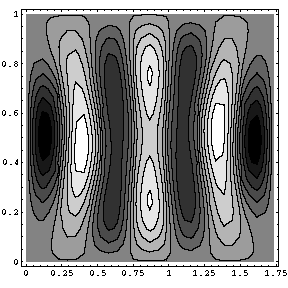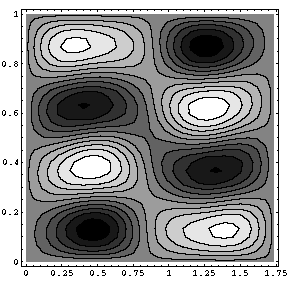
 White/black indicate +/- signs of the wavefunction extrema.
White/black indicate +/- signs of the wavefunction extrema.
A cyclic Berry phase of π corresponds to a sign change of the corresponding eigenstate: the "jump" of the plotted wavefunction when the loop restarts reflects this cyclic phase.
Consider in general the parallel adiabatic evolution of the nondegenerate normalized eigenstates |ψi(r)> of a parameterized Hamiltonian H(r). The idea that, with a suitable definition, the phase of the scalar product <ψj(r1)|ψj(r2)> can be measurable dates back to the pioneering work of Pancharatnam[Pancharatnam]. When r1=r2 and the state |ψj(r)> is transported adiabatically along a closed loop, we have the usual cyclic Berry phase. Since its formalization, considerable work has been devoted to interpretation generalization, and experimental determination of these geometric phase factors. Surprisingly, for r1&neq;r2, the phase of <ψj(r1)|ψk(r2)> between two different eigenstates has not been equally well investigated so far[simon:note].
In our figure above, this happens exactly at mid path: the evolution starts from a wave of type {2,4} (i.e. with 2 semi-oscillations in the horizontal direction and 4 in the vertical one). It then undergoes some mixing, to become a {7,1} wave at mid way. Finally it evolves to become again {2,4}, but with the changed sign (its Berry phase discussed above). It is known by elementary Fourier analysis that the waves {2,4} and {7,1} are indeed orthogonal.
As the figure below indicates, it turns out that, following the same path, the state {7,1} goes at mid path to {2,4}: the two states exchange.
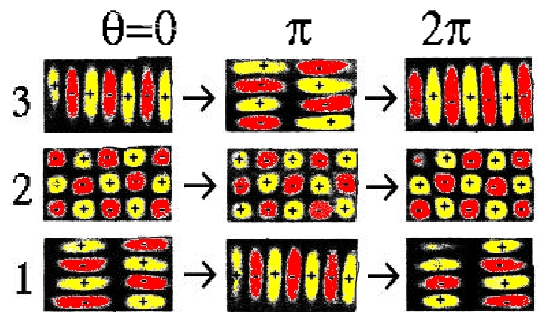 The observed initial (θ=0), intermediate
(θ=π) and final (θ=2π) eigenstates of the microwave cavities deformed
following adiabatically the path of Ref. [Lauber94]. These three eigenstates of the rectangular
resonator get degenerate for the undistorted rectangular geometry.
The observed initial (θ=0), intermediate
(θ=π) and final (θ=2π) eigenstates of the microwave cavities deformed
following adiabatically the path of Ref. [Lauber94]. These three eigenstates of the rectangular
resonator get degenerate for the undistorted rectangular geometry.
Clearly, at mid path, each state has no meaningful phase relation with respect to the state at departure. However there should be some phase relation hidden somewhere in the adiabatic evolution. The purpose of this work is to determine the measurable quantities associated to the phases of the off-diagonal matrix elements <ψj(r1)|ψk(r2)> for a general open path in the parameter space connecting r1 to r2.
An illustration of these ideas is available as a pdf presentation. More details are available in the References below.
More recently in collaboration with prof. H. Rauch's group of experts in neutron interferometry, at the ILL we measured the off-diagonal phase of the neutron spin wavefunction, confirming these theoretical predictions.