Immaginiamo di voler calcolare la somma S = a1 + a2 + ... + a16 , per un totale di 15 addizioni, con un calcolatore parallelo dotato di pprocessori.
Chiameremo Tp (con p maggire o uguale ad 1) il tempo impiegato (dall'elaboratore parallelo con p processori) per il calcolo di S da un algoritmo parallelo che utilizza p processori.
Assumendo che il tempo macchina per elaborare
una singola addizione sia preso come unità di riferimento: t=1,
si ha banalmente che T1
= 15.
Consideriamo ora il caso p=2:
-----------------------
(p=2)
il modo migliore per ripartire i calcoli tra
i 2 processori è quello di far elaborare al processore 1 la somma
y1 = a1 + a2 + ... + a8
contemporaneamente alla elaborazione della somma
y2 = a9 + a10 + ... + a16
da parte del processore 2 (step 1);
il tempo per elaborare y1 ed y2 contemporaneamente
è 7.
A questo punto uno dei due processi esegue la
somma
S = y1 + y2
(step 2) mentre l'altro rimane inattivo, ed il
tempo totale impiegato per ottenerla è chiaramente T2
= 8.
-----------------------
Passiamo ora in successione i casi p=3,
p=4, p=8:
-----------------------
(p=3)
step 1:
y1 = a1 + a2+ ... + a5;
y2 = a6 + a7 + ... + a10;
y3 = a11 + a12 + ... + a15
;
tempo parziale 4.
step 2:
z1 = y1 + y2;
z2 = y3 + a16;
tempo parziale 1, ed un processore rimane inattivo.
step 3:
S = z1 + z2;
e due processori rimangono inattivi.
Tempo totale T3
= 6.
-----------------------
(p=4)
step1:
step 1:
y1 = a1 + a2+ ... + a4;
y2 = a5 + a6 + ... + a8;
y3 = a9 + a10 + ... + a12
;
y4 = a13 + a14+ ... + a16
tempo parziale 3.
step 2:
z1 = y1 + y2;
z2 = y3 + y4
tempo parziale 1, e due processori rimangono
inattivi.
step 3:
S = z1 + z2.;
e 3 processori rimangono inattivi.
Tempo totale T4
= 5.
-----------------------
(p=8)
step 1:
y1 = a1 + a2;
y2 = a3 + a4;
y3 = a5 + a6;
y4 = a7 + a8;
y5 = a9 + a10;
y6 = a11 + a12
;
y7 = a13 + a14;
y8 = a15 + a16
tempo parziale 1.
step 2:
z1 = y1 + y2;
z2 = y3 + y4;
z3 = y5 + y6;
z4 = y7 + y8
tempo parziale 1, e quattro processori rimangono
inattivi.
step 3:
w1 = z1 + z2;
w2 = z3 + z4
tempo parziale 1, e sei processori rimangono
inattivi.
step 4:
S = w1 + w2.;
e 7 processori rimangono inattivi.
Tempo totale T8
= 4.
-----------------------
Come si puo' notare all'aumentare del numero
di processori il calcolo di S
viene
eseguito sempre piu' velocemente, ma l'efficienza del calcolo
contemporaneamente diminuisce poiche' sempre piu' processori rimangono
inattivi una volta elaborate la maggior parte delle addizioni necessarie
al calcolo della somma.
Seguono ora alcune definizioni o concetti
base per l'analisi delle prestazioni di una elaborazione parallela:
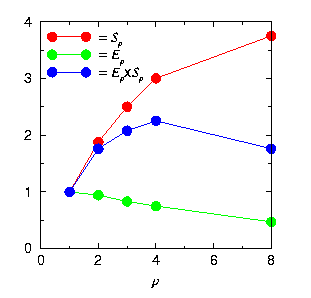
| p | Tp | Cp | Sp | Ep | Ep x Sp |
| 1 | 15 | 15 | 1 | 1 | 1 |
| 2 | 8 | 16 | 1.88 | 0.94 | 1.76 |
| 3 | 6 | 18 | 2.5 | 0.83 | 2.08 |
| 4 | 5 | 20 | 3 | 0.75 | 2.25 |
| 8 | 4 | 32 | 3.75 | 0.47 | 1.76 |
il prodotto Ep x Sp e' massimizzato dalla scelta di 4 processori:
