LEGGE DI AMDAHL ('67)

Immaginiamo ora di avere un codice composto da una frazione f  perfettamente parallelizzabile e da una frazione 1-f che invece non puo' essere parallelizzata e quindi deve essere eseguita in modo seriale:

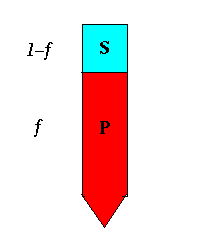
immaginiamo inoltre di avere un elaboratore parallelo composto da p processori.
Se con T1 si identifica il tempo necessario per elaborare in modo completamente seriale il codice in questione, avremo che:

A questo punto siamo in grado di  ricavare Tp e cioe' il tempo necessario per elaborare l'intero codice su di un calcolatroe parallelo con p processori:

Tp = (1-f) T1 + f T1 / p = T1[ f + (1-f) p ] / p

E' possibili ora ricavare lo speed-up:

Sp = T1 / Tp = p / [ f + (1-f) p ] = 1 / [ f/p + (1-f) ]

utilizzando un numero sempre piu' elevato di processori e' possibile far tendere a zero il rapporto f/p. Si ottiene percio' che

Sp e' minore o al massimo uguale ad  1 / (1-f).

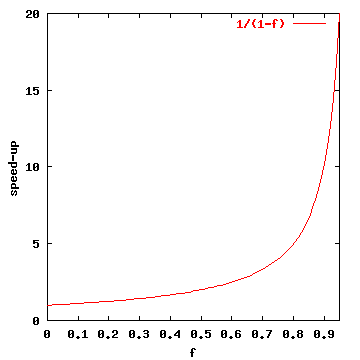
Questa e' la Legge di Amdahl, la quale inpone un limite superiore per il possibile speed-up in un codice in cui esiste una parte irrimediabilmente seriale. E' la fine del calcolo parallelo?

No! Spesso la frazione non parallelizzabile (1-f) tende a zero quando le dimensionei computazionali del problema da parallelizzare aumentano; tornano quindi ad essere possibili speed-up elevati.

E'  ovvio comunque che questa e' un discorso molto astratto ed in realta' l'analisi della situazione e' piu' complessa.
Ad esempio non abbiamo mai preso in considerazione il fatto che quando i processori cooperano in modo parallelo per elaborare una certa quantita' di calcoli, esiste un tempo speso nel comunicare i risultati parziali necessari spesso ai vari processori per poter continuare l'elaborazione.
Le prestazioni di  una elaborazione parallela vengono quindi a dipendere anche da  quante informazioni si devono scambiare i vari processori durante l'elaborazione parallela e dalla velocita' con cui la rete di interconnessione scambia i dati tra i vari processori.

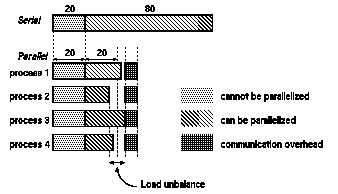
Per quanto riguarda il degrado delle prestazioni che nascono dalla necessita' di comunicare dati durante l'elaborazione parallela, si deve notare che questo spesso puo' comportare per alcuni processori dei punti morti in cui questi rimangono inattivi perche' in attesa di dati da altri processori sottoposti ad un carico di lavoro maggiore, sono problemi legati alla sincronizzazione tra i processori:

Per quanto riguarda invece la velocita' con cui vengono scambiati i dati tra i processori, due sono le proprieta' della rete di interconessione che risultano essere cruciali per le prestazioni dell'elaborazione parallela:

In presenza di latenza (come per ogni rete di interconnessione reale) la larghezza di banda effettiva Leff diviene:

Leff = Dm / Ttot = Dm / ( l + Dm/L ) = L / ( 1 + L l / Dm )

dove Ttot e' il tempo totale di comunicazione, mentre Dm e' la dimensione del messaggio;

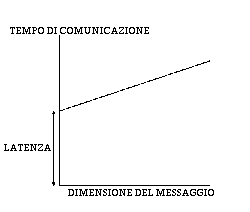
quindi Leff tende ad L solo se le dimensioni del messaggio Dm tendono all'infinito.

Per concludere una buona parallelizzazione si ottiene ogni volta che: